Acoustic energy
For further reference we now consider the acoustic energy. Following the original approach of Kirchhoff, we start from the linearized mass and momentum equations:
|
dE ті f 1 ~0t + ‘ = (pqcq)2T0 V ds |
|
with the acoustic energy density E defined by : E =1 PQfff + (P’>2 |
Then we multiply the mass conservation law by p’/pQ and add the in-product of the momentum equation with the velocity v’, to find:
and the intensity I defined by:
![]() f = p’v’ .
f = p’v’ .
It should be noted that this derivation assumes that we did not neglect any relevant quadratic terms when using the linear approximation for the mass and momentum equation. This approach appears to be valid only for the case considered, i. e. of a uniform stagnant reference state [Morfey (1971), Landau and Lifchitz (1987), Pierce (1990), Myers (1991)].
Equation (66) clearly shows generating acoustic energy requires that a volume source should be placed at a position with a large acoustic pressure. A force needs an acoustic velocity to generate acoustic energy.
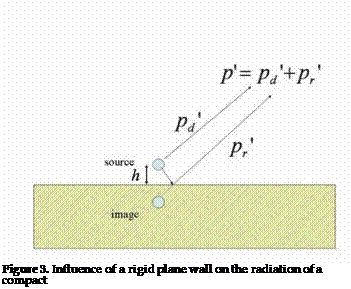 |
Considering a compact pulsating sphere near a rigid plane wave kh << 1 (Figure 3), we observe that due to reflection at the wall the amplitude of waves reaching an observer in the far field is roughly double the amplitude we would find in free space. Hence, the intensity is four times larger than in free space. However, the source only radiates into a half space, so that the time averaged power < P > generated by the source is doubled. This result can also be understood as a result of the doubling of the pressure fluctuations surrounding the source, due to reflection at the wall, which, following our energy corollary doubles the generated power. This implies
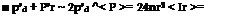
![]() sphere placed near the wall: p’ 2 x 4nr2 <
sphere placed near the wall: p’ 2 x 4nr2 <
PoC
that the radiated power is doubled compared to free field conditions. This example stresses the fact that the sound power does not only depend on the source but also on the surroundings of the source.











