Differential Conservation Equations

1.4.1 Divergence forms

Using Gauss’s Theorem for a general vector field quantity v(r),

© v ■ П dS = V ■ v dV (1.31)

pV, the integral mass equation (1.27) can be restated in terms of only a volume integral.

dp

^ + V-(pV) dV = 0 (1.32)

Since this must hold for any control volume, the integrand must necessarily be zero for every point in the flow. The result is the divergence form of the differential mass equation.

The same process applied to the integral momentum and vergence differential forms.

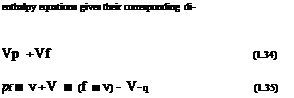– Pt-

+ V ■ (pV = 4,. +

1.4.2 Convective forms

Combining {momentum equation (1.34)} — V{mass equation (1.33)} and simplifying produces the con­vective form of the momentum equation,

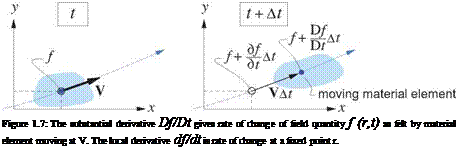is the substantial derivative, which is the rate of change of any field quantity () as observed by a fluid element moving with velocity V, as shown in Figure 1.7.

Combining {enthalpy equation (1.35)} — ho{mass equation (1.33)} and simplifying produces the convective form of the enthalpy equation.

The mass, momentum, and enthalpy equations above, either in the divergence or convective forms, are collectively called the Navier-Stokes equations, although historically this term was originally first given to only the momentum equation (1.36) in its incompressible form, which will be considered in Section 1.8.

1.4.3 Surface boundary conditions

The appropriate boundary conditions for a viscous flow at a solid surface are the no-slip condition on V, and either a temperature condition or a heat-flux condition on h.

V = 0 (on solid fixed surface) (1.39)

either h = Cp Tbody (on surface with known temperature) (1.40)

or q ■ n = 0 (on surface at thermal equilibrium with fluid) (1.41)

For the idealization of an inviscid flow, the appropriate solid surface boundary condition is the following flow-tangency condition on V. No solid-surface boundary condition required for the temperature.