Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
ENSEMBLE AVERAGE
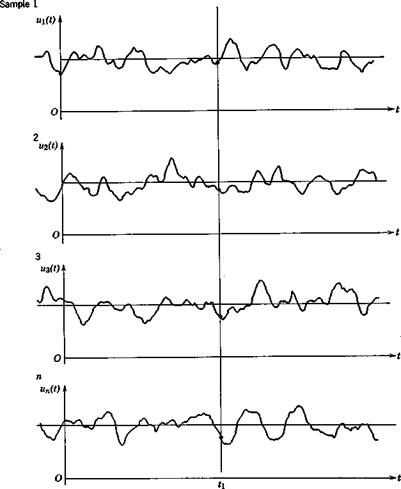
In the above discussion, the time average of a single function was used. Another important kind of average is the ensemble average. Imagine that the physical situation that produced the random variable of Fig. 2.4 has been repeated many times, so that a large number of records are available as in Fig. 2.5.
|
Fig. 2.5 Ensemble of random variables. |
The ensemble average corresponding to the particular time is expressed in terms of the samples u^tj) as
<«(<i)> =lim (u(tv n)) =lim – [w1(i1) + м2(У ‘ ’ ’ (2.6,3)
n-* oo n-* oo 71
If the process is stationary, (ад(^)) — (и), independent of tv The process is said to be ergodic if the ensemble and time averages are the same, i. e. (и) = й. This will be the case, for example, if the records are obtained from a single physical system with random starting conditions. In this book we are concerned only with stationary ergodic processes.
