Flow Past Arbitrary Airfoils

1.4.1 Kutta-Joukowski Lift Theorem

The theory of conformal mapping tells us that it is possible to map any simply connected profile onto a circular cylinder. In the transformation, the flow past the profile maps into the flow past a circular cylinder derived earlier. The far field flow is preserved. The inverse transformation will therefore describe the exact solu­tion of the flow past the original profile. One such transformation is the Joukowski transformation

z	z
Fig. 2.12 Cylinder plane (X, Z) and physical plane (x, z)
(2.39)

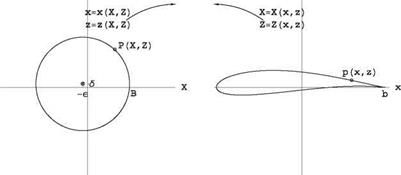
where (x, z) represent the physical plane of the profile and (X, Z) the plane of the cylinder. Notice that the transformation preserves the far field (i. e. x ^ X and z ^ Z far from the origin). A cylinder of radius r0, where r2 = (a + e)2 + S2 centered at X = —e, Z = S and passing through point B located at X = a, Z = 0 maps onto a family of Joukowski airfoils depending on e and S. The profile has a cusp at the trailing edge, point b, image of point B. See Fig. 2.12. In the figure, p is the image of P through the transformation.

The polar coordinate representation of the cylinder is

X = r (в) cos в, Z = r (в) sin в (2.40)

where r (в) = —(e cos в — S sin в) + л/a2 + 2ea + (e cos в — S sin в)2.

Through the mapping, the parametric representation of the Joukowski profile is obtained

(2.41)

In the mapping, the doublet and potential vortex contribute to a distribution of singularities (sources, sinks and vorticity distributions) inside the profile. In the far field, however, the leading terms in the perturbation velocity field correspond again to a doublet (closed obstacle) and a potential vortex with the same net circulation Г. To calculate the force on an arbitrary profile, one can apply the momentum theorem to the domain inside a large circle C of radius R centered at the origin

Fig. 2.13 Control surface for application of the momentum theorem

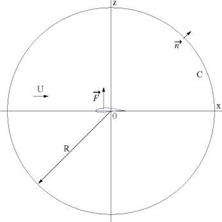where F’ represents the force per unit span applied by the fluid to the profile. See Fig. 2.13.

We will assume that any solution near C can be expanded asymptotically as

Let n = (cos в, sin в) then

The force will be evaluated in the Cartesian coordinate system. The Cartesian form of V is

where i and k are the unit vectors of the x and z-axis respectively. Hence, the first term in the integrand Eq. (2.42) reads

When integrated on the circle, the cos в and sin в cos в terms vanish and there remains only

A uniform flow produces on a cylinder of arbitrary cross-section a lift force per unit span L’ = pU Г that is proportional to the circulation Г around the profile. The orientation of the force is obtained by rotating the incoming flow velocity vector 90° opposite to the circulation.

Another way to derive this theorem is to consider a control volume as in Fig. 2.14.

If the top and bottom boundaries of the control volume are far from the obstacle (distance H), the pressure will have the atmospheric value and the velocity will be the undisturbed velocity. The circulation, however, will not vanish as it remains constant over any closed curve enclosing the obstacle. The momentum theorem, Eq.(2.42), in projection on the z-axis reduces to

where pressure does not contribute because it is atmospheric on the upper and lower surfaces and its action is perpendicular to the z-axis along the side boundaries. Since u and w are of order 0 ^-^===^ or higher, where D (H > D) is the distance of the side boundaries to the z-axis, the result can be expressed as

L ‘ = pU Г + o(DT+H5) <2-54)

The final result is obtained by letting D ^ro. A similar approach, with a control volume where now D > H can be used to prove that the drag D’ = 0. This result is consistent with the calculation of the lift over the cylinder, since with the Joukowski transformation or any transformation of the obstacle to a cylinder that preserves the far field, the lift over the obstacle is the same as the lift over the cylinder at the same angle of incidence. Furthermore, as a consequence of the conservation of momentum, the lift is proportional to the circulation as L’ = pU Г and the drag D’ = 0.

1.4.2 The d’Alembert Paradox

The d’Alembert paradox results from the fact that when a profile is moving at uniform velocity in a fluid, the resulting force is perpendicular to the velocity. The drag is zero. This result is consistent with the inviscid, frictionless fluid assumption. But in fact, with all real fluids, there is friction along the surface of the profile and there will be <a small) drag. The analysis of viscous forces in the boundary layer will resolve this paradox.

Fig. 2.15 a Profile that does not satisfy the K-J condition and b Profile that does satisfy the K-J condition