GLOSSARY OF TERMS

There are some comparatively recent publications avail­able (9,a) listing and defining aero-space terms. In the following are some of them referring to lifting airplanes.

An Airfoil (British “aerofoil”) is usually meant to be a rectangular wing model, used to determine lifting charac­teristics of particular airfoil or wing sections. There may be some doubt whether the airfoil has a leading edge or a “nose”. The latter evidently comes from the two-dimen­sional thinking (on paper) in terms of airfoil-section shapes. One also talks about “points” along the surface. So there is some confusion between 2- and 3-dimensional terms.

Wing. It seems that birds have a pair of wings, while an airplane has only one. This wing has a pair of “panel”, however. Wings used to be straight; they are swept now, that is in high subsonic speed airplanes. The shape pre­ferred in super-hypersonic Bight is the “delta” wing. The most important geometric characteristic of wings is their aspect ratio

A = b/c = b2 /S = S/c2 (1)

where c = (mean aerodynamic chord) = S/b.

S = wing area b = wing span

Aerodynamic Centerj In Europe, there were many decades where the pitching – moment was measured and defined about the leading-edge “point”. Since theoretically the lift can be expected to be centered at % of the chord, that is at x = 0.25 c, it became customary, however, to indicate the moment about this point. While in the European definition, the coefficient may thus be in the order of -0.25 C(_ (indicating that the lift would cause the airfoil to pitch down, about the leading edge) – the coefficient may be C^/4 = (+ or -0.01) CL, for example, thus indicating that the lift force is centered at a point (0.01 Cu) ahead or aft of the quarter-chord point. There is also a point on or near the chord of every airfoil (or a trans­verse axis in every airplane without a horizontal tail) about which the moment coefficient is constant (when increasing the lift coefficient). This point is the aerodynamic center (3,d); see Chapter II on airfoils.

(7) Biot (a friend of vonKarman), “Drowning in Complexity”, Mech Engg 1963 p 26; says that engineering “ability is intuitive, resembling artistic talent”, while “formal knowl­edge rather than understanding, is not favorable to creative talent”.

Mean Aerodynamic Chord. Considering a wing with an arbitrary plan-form shape, the mean aerodynamic chord is that of “an imaginary rectangular wing that would have pitching moments the same as those of the actual airfoil or combination of airfoils” (such as a biplane). The “mac” is geometrically defined by

c = (2/S) rb/2czdy (2)

J0

In case of a swept wing, the spanwise position is of great importance. It is normally assumed that the lift distribu­tion be elliptical. The load i$ then concentrated at

у = (4/3 тт) b/2 = 0.424 (b/2) (3)

from the centerline. Of course, the lateral center ;.s “al­ways” somewhere else. In particular, in rectangular and/or swept-back wings it is outboard of 0.424. It would there­fore be just as well to determine the aerodynamic center as a geometrical point as in figure 2 in Chapter XI.

Lift Angle. Lift as a function of the angle of attack is usually given in form of the derivative (dCL /dot ). How­ever, in wings with finite span, the angle required to produce a certain lift coefficient consists of at least 2 components. Including the influence of longer chords and the proximity of the ground (in airplane wings) or the water surface (in hydrofoils), there are at least 2 more additional terms of the angle of attack to be taken into account. It is therefore logical to use what we call the “lift angle”, namely the derivative (dor /dCL) = (dor /dCL.), + (da /dCL )г and so on. The equations describing li ft are thus simplified, and each component can be treated indi­vidually.

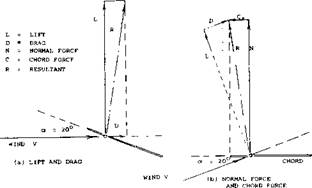
Forces. As shown in figure 1, in the wind-tunnel system, the normal-force coefficient of a wing is

CN =CL cos a +CD sin a (4)

where the second term is usually quite small. However, in the longitudinal (or chordwise) direction, the two com­ponents of the longitudinal force

Cx = CD cos or — CL sin a (5)

are of equal importance. In fact, if CD = 0.01 foi ex­ample, aCL = (dCL /dor ) sin a ^ 4(0.0025) is sufficient to make Cx = zero. The corresponding values are a = 0.05 ~ 3 , and CL = 0.2. In other words, at larger angles of attack, Cx turns negative, which means directed for­ward along the wing chord. – It might sometimes als:>be necessary to consider the resultant of the components. This “total” force corresponds to

Figure 1. Aerodynamic forces and their components in an airfoil section (or of an airplane). and it should not be confused with the normal force, of a wing for example. As shown in the illustration that force can also be split up into the normal force (equation 4) and a longitudinal or tangential component.

A Vortex has a strength of circulation

Г = w2r in (m2/s) (7)

This means that (wr) = constant, and w~l/r. The circum­ferential speed w thus varies with the radius r in the same manner as that of a planet or satellite. Theoretically, therefore, w — oo in the center of the vortex. In reality, viscosity produces a rotating core, where w ^ r. The circulation of a wing is

Г = 0.5CU Vo = w2r тт (g)

and this circulation is maintained in the pair of trailing vortices. We obtain the speed ratio

V/w = 41Г (r/c)/Cu (10)

Since formation and diameter of that core is a matter of viscosity and the disturbance (separation) of the flow at the lateral edges of a wing, experimental results are better than any estimates. In this respect, see Chapter III.

Irrotational is a flow, and particularly that in a vortex, where the air particles move in the manner as the cars in a Ferris wheel (G. W.G. Ferris, engineer, 1859 to 1896). It is difficult, however, to “tie in this analogy with the mathe­matics of the flow”. Indeed, it does not seem to be of any practical consequence whether the molecules rotate about their own axes. It is emphasized, however, that any rota­tional flow involves losses of energy, through turbulent mixing and possibly by way of flow separation. Might “irrotational” be a misnomer, insofar as absence of viscosity would be more important?

Potential Flow. In contradistinction to a streamline, a streamtube is something real. The constant volume flow of air which it is carrying, is its “stream function” Q in (m /s). In theoretical analysis, the tube is said to gain the

potential = (Q/S)x = V x in (m2/s) (11)

This quantity can be visualized as that of a mass travelling upward at the speed V, thus gaining potential energy. In any direction normal to a streamline, the potential is constant. In the direction of the streamline the stream function, is constant, while the potential may be said to be a level, the variation of which produces a speed differ­ential. All this applies only to “irrotational” flow, as explained above. When, under conditions of no loss of momentum, the diameter of a streamtube increases, the velocity decreases, and the rate of gain of the potential decreases accordingly. However, the rate increases again, when the velocity increases, for example as a consequence of a negative pressure gradient.

The Momentum of a solid body moving at the speed V, is

momentum = mass (speed) in (kg m/s) (12)

It is an indication for the inherent energy of that body, or the work which the mass can produce when stopped. Thus

work = energy = momentum (speed)

in (N – m) = (kg-ma/se) (13)

In a stream of air, we do not have a finite mass. Rather, in case of a propeller or a jet engine, we have a mass flow in kg/s. The thrust produced is

T = (mass flow) (added speed);

in N = (kg-m/s2) ( 14)

In the case of a lifting wing, momentum is transferred onto the passing stream of air by adding a vertical com­ponent of velocity. Momentum is thus added, not in the direction of flow, but essentially at a right angle to it. Accordingly, lift is proportional to the vertical or down – wash velocity w

L ~ (mass flow) w; in N = (kg-m/s2") (15) [5]

Pressure. Various types of pressure in fluid-dynamic flow are explained in “Fluid-Dynamic Drag”. Because of their importance, the following is added (or repeated) at this point. Absolute pressures, such p = 2116 lb/ft2, or = 1010 N/mz, as in the ambient standard atmposhere at sea level, are often used in gasdynamics (at supersonic speed). With­in the range of subsonic aerodynamics, pressure differences are usually considered. An example for such a differential is the “gage” pressure in the tires of an automobile, measured against the atmosphere. Of course, lift is the result of pressure differences between the upper and lower side of a wing; and it would not make any difference whether the pressures involved would be measured as absolute or relative quantitites. In a wind tunnel, for example, it is more convenient and accurate, however, to measure them as gage pressures, that is as positive or negative quantities as against the ambient (atmoshperic or tunnel) pressure. To be correct, the pressure coefficient should thus be written as

CP = (p-Pa)/q = 4p/q (16)

where “a” indicates “ambient” or “atmosphere”, and zip = pressure differential.

Stagnation Point. Strictly, an airplane may only have one point (at the nose of the fuselage) where the air particles really come to rest. No doubt, a configuration with a swept-forward wing will have a minimum of three such points. For practical purposes, a straight leading edge would have a stagnation “line”, however. In incompressi­ble fluid flow, the pressure increment at the stagnation point is the “dynamic” pressure

q = 0.5$>V2 (17)

In spite of its name, this pressure is thus basically a static pressure differential; namely between that at a stagnation point (where velocity = zero) and the ambient level. At higher speeds in gases, the pressure at the point is higher, however, than according to equation (17), because of compressibility of the fluid or air used, and on account of an increase in its temperature. That pressure is called the impact pressure. The dynamic pressure must then be con­sidered to be a dynamic potential of the stream of air against an obstacle; and all coefficients (at least in sub­sonic aerodynamic flow) are still referred to that pressure. One practical reason for doing so, is skin-friction, the coefficient of which reduces with the Mach number (be­cause of increasing temperature and increasing density within the boundary layer). Another reason is the fact that the value of negative pressure coefficients does not increase in proportion to that of the stagnation pressure. The only place where forces et cetera, are found to be proportional to the impact pressure, is in hypersonic gas dynamics.

“Negative” Pressure. One of the discoveries of experi­menters such as Lilienthal (before 1900) was the fact that “suction” over the upper side of a properly cambered airfoil contributes more to lift than the “positive” pres­sure at the lower side. Of course, in absolute terms, pressure at the upper side was simply more lower, than that at the lower side was higher. This balance of pressures can be dramatized when thinking of a pump in a farm­yard. When moving the plunger up, it does not exactly draw water up. Rather, the piston tries to create a vac­uum; and the atmospheric pressure pushes the water up from below. In fact, when the waterlevel in the well is more than some 10 m or 34 below the pump, no water can be pumped at all. A similar thing happens in hyper­sonic flow (at M -^-oo) where the pressure on the upper side of a wing is zero (vacuum) and “all” of the lift is produced by positive pressure at the lower side.

“Pressure Distribution” generally indicates the distribu­tion of static pressure over the upper and lower surfaces of a wing, plotted particularly in chordwise direction. In contradistinction, the term “load distribution”, for ex­ample along the span of a wing, indicates that of the normal force which is equal to the pressure differential between lower and upper side. For the sake of correlation with the sides of airfoil sections, their pressure distribu­tions are usually plotted with the negative pressure co­efficients developing along the upper section side up, and the positive values on the lower side down. This procedure could be made mathematically perfect when plotting (Y+/V) = 1 – Cp_}_, where (+) indicates the specific

location. For V+ = V, we then find Ср^= 0; or for (Vf /V)2 = 0, we have C = +1.

Hydrodynamics. The term “hydrodynamics” is used in aerodynamics, to indicate that compressibility is absent or negligibly small. There are devices, however, actually used in water, producing “lift” in a manner at least similar to that of wings in air. In ships and boats, we have rubbers, fins, control surfaces (in submarines) and finally hydro­foils. As far as their fluid-dynamic characteristics are the “same” as in air, a chapter of this book is devoted to their presentation. Since “lifting ” characteristics in water can also be different or limited (by cavitation or ventilation), another chapter is added describing these effects.

Other Terms, explained in chapter I of “Fluid-Dynamic Drag” are:

Boundary layer, developing along surfaces;

Circulation around wings, as in equation (8);

Compressibility in air flow, at higher speeds;

Down wash, developing behind wings;

Induced angle of attack, in wings;

Rotation, as in the core of a vortex;

Separation and Wake Flow, associated with pressure drag;

Streamlines and Streamtubes, forming a flow pattern; Turbulence, developing in boundary layers;

Vortex, lifting and trailing, as mentioned above; Vorticity, in viscous fluid flow, equivalent to “rotation”.

Similarity Laws. Many fluid-dynamic similarity laws are needed to correlate model test results with full scale tests. The more common parameters used are Reynolds number, the ratio of the inertia forces in the fluid to the viscous forces, and Mach number, the ratio of the velocity of the body to the velocity of sound. The following additional correlating parameters are explained in “Fluid-Dynamic Drag” and are also of importance:

• Lift, drag and movement non-dimensional coeffi­cients

• Cavitation Number in water

• Fronde Number, at the surface of the water.

Regarding the various laws of similarity, there may be conditions where at least two of them are involved at the same time (such as Reynolds and Mach number). There are, on the other hand, areas where one or the other is not important (such as compressibility in water). We have to be sure, however, that we do not cross critical boundaries, between different modes of fluid behavior (such as the critical Mach number, or the number of incipient cavi­tation).

Metric System. The atomic physicist Edward Teller is reported to have said that “the United States may lose the space race by an inch”. Meanwhile, the U. S. Army is measuring distance in meters, NASA’s space laboratories are using the metric system, and the Bureau of Standards has adopted it. The metric system is thus generally used in this book. Conversion factors and constants may be found in (10,a), which is readily available as well as many other sources.

(9) Regarding aeronautical terminlogy, see:

a) Adams, Aeronautical Dictionary, NACA (1959).

b) Books such as Diehl (20,b) and Wood (20,c) (20,h).

d) Wenzelberger, Mechanical Analogy, Award Paper IAS Stu­dent Conference (1957).

e) NAVAER (Operations) Flight Manual (1957); reproduced by Fed Aviation Agency.

f) Nayler, Dictonary Aeronautical Engg, Philosophical Li­brary New York.

(10) The international system of units (SI):

a) Mechtley, International System ot Units, NASA SP-7012 (1964). Available Superintendent of Documents, U. S. Gov­ernment Printing Office, Washington, D. C. 20402.

b) Hamilton, "Going Metric”, The Engineer 1966 p 150.

c) Miller, Calibration in Hotshot Tunnel, NASA TN D-3278 (1966).

d) See also ”The Standard Atmosphere” under (11 ,e).

1 – 7

For convenience, symbols as used throughout this texl, are listed at the very end of the book. In this manner, the meaning of any one symbol can easily be found, without searching through this first chapter.

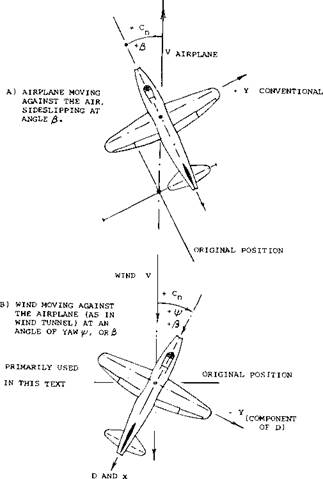
Directions. There are two geometric systems considered and used in airplane aerodynamics.

a) Body axes (as in part (a) of figure 2) could logically be used by a pilot flying in an airplane; and they are used when analyzing motions of airplanes. It should be noted that x is positive forward from the CG, and Z positive in the down direction (where the airplane tends to fall). According to standard notation roll angle and moment “L” are positive in right-hand screwdriver direction.

b) In a wind tunnel, the geometric system is defined by the direction of the airflow (as in part (b) of figure 2). Lift L and drag D as produced by that flow are positive in their common sense. Fortunately, the angles of pitch (of attack) and or roll are defined positive in the same direc ­tions in the two systems.

The difference between the two systems is shown in figure 2. In part (a) the airplane moves forward and sideways (sideslipping) in positive directions. In part (b) of the illustration, the airplane is stationary (suspended in a wind tunnel) and set at an angle of yaw. The wind direction is positive. About the vertical axis, the angle of “sideslip’” is defined to be positive when the airplane moves to the right (starboard) side. This definition is opposite to the angle of yaw under (b), where the airplane is turned to the right, so that the wind comes from the left. Nevertheless, the corresponding moment is still the “yaw moment” as under (a). The corresponding angle is the angle of yaw Regarding the sign, the aerodynamic engineer is primarily interested in whether the yaw moment helps turning when deflecting the ailerons or not. Thus the positive direction as in system (a) conveys the right meaning, while a nega­tive yaw moment can also be called “adverse”, even if by definition, it is positive in system (b). The same combina­tion of signs for roll and yaw moments goes for a motion initiated by rudder deflection. — Since in this text, forces and moments, rather than motions, are primarily con­sidered, the wind-tunnel system (b) is predominantly used. As in general usage, some inconsistencies (some mixup between the two systems of reference) seem to be unavoidable, however. — There is still another direction used in aerodynamic language. According to Webster, down — and upstream indicate a direction, rather than a location. To identify the ends of a fuselage, one shoulc., therefore, use the words forward and aft or rear; or in case of wing edges, leading and trailing.

Figure 2. Systems of axes, forces, moments, used in analysis and presentation of aerodynamic characteristics of airplanes.

(11) Physical properties of air as a function of altitude:

a) Values by International Civil Aviation Organization (1952), NACA Rpt 1235.

b) Atmospheric properties are presented at length in (20,c)

(20,h).

c) Properties are presented in chapters I & XIX of “Fluid – Dynamic Drag”.

d) Information on viscosity is found in chapter I of “Fluid – Dynamic Drag”.

e) Minzner, US Standard Atmosphere 1962, US Government Printing Office.

0 Density Variations, Army R&D Labs Monmouth Rpt 2393 (1963); AD-425,913.

g) Valley, “Handbook Geophysics and Space”, McGraw-Hill 1965.

(13) Regarding various types of pressure see:

a) Aiken, Pressures and Airspeeds, NACA Rpt 837 (1946).

b) Atmospheric, as a function of altitudes, see (11 ,a, b,e).

c) The pressure p in figure 4 is of importance for the performance of engines.

Angle of Attack. In the two systems discussed, the angle of attack or pitch has one and the same sign. A British synonym is “incidence”. In the United States, however, the angle of incidence (or that of setting) is meant to be that of the wing (or horizontal-tail) chord against the fuselage. Corresponding to the sign of these angles, posi­tive when “nose-up” and when increasing the lift, idle longitudinal or pitch moment is automatically called posi­tive when tending to increase the angle of attack. As a consequence, longitudinal stability in terms of (dCm/dCt, ) or (dC<_ /dor ), has a negative sign when the airplane is stable. – Still another longitudinal angle is that of attitude, that is the angle of the airplane axis against the horizontal. The angle of climb or of gliding is inclu ded in this angle.

Positive/Negative Values. For the aerodynamic engineer, there are various considerations where the sign of a para­meter is in doubt. We see in figure 2 that in one system of reference, drag is positive, while in the other, thrust is positive. Also, which one is positive, lift or weight = g (mass)? Regarding the induced angle of attack, we can write

Cu = 2 тґ(оіг – о^ ); orCL = (dCL /dof ) + о/; ) (18)

where оГ£ = two-dimensional or sectional angle. In a similar manner, it can be argued whether the angle of downwash behind a wing is positive or negative. Certainly, this angle is down in the wind system, but the foil requ ires an additional positive angle of attack. In all such ex­amples, we have action and reaction, or the compensation of fluid-dynamic forces or moments by “static” ones. The problems can be resolved by accepting absolute values of the many dimensions involved; and the typical engineer is doing that daily, without even thinking about it. The sign of a quantity becomes critical, however, when pitching one force (for example) against another one, or when adding quantitites (such as lift and weight, for example).