METHODS FOR THE INVERSE TRANSFORMATION

THE USE OF TABLES OF TRANSFORMS

Extensive tables of transforms (like Table 2.3) have been published (see Bibliography) which are useful in carrying out the inverse process. When the transform involved can be found in the tables, the function x(t) is obtained directly.

THE METHOD OF PARTIAL FRACTIONS

In some cases it is convenient to expand the transform x(s) in partial fractions, so that the elements are all simple ones like those in Table 2.3. The function x(t) can then be obtained simply from the table. We shall demonstrate this procedure with an example. Let the second-order system of Sec. 2.4 be initially quiescent, i. e. x(0) = 0, and ж(0) = 0, and let it be acted upon by a constant unit force applied at time f = 0. Then /(f) = 1(f), and /(.s) = 1 js (see Table 2.3). From (2.4,4), we find that

ф2 + 2 £cons + con2)

Let us assume that the system is aperiodic: i. e. that £ > 1. Then the roots of the characteristic equation are real and equal to

Z12 = n ± со’

Therefore

m = w. + m – + ід2(я2 – At) s s Ai s • A2 By comparing these three terms with items 3 and 8 of Table 2.3, we may write down the solution immediately as

x(t) = — H———————————– ——- e A±A2 A| (А і A2) A2(A, ■ A2) = J_ [l, n – e(n+a>’)t _ n + °> ‘еЫ-т’Н ton2 L 2w’ 2ft)’ .

(2.5,5)

HEAVISIDE EXPANSION THEOREM When the transform is a ratio of two polynomials in s, the method of partial fractions can be generalized. Let

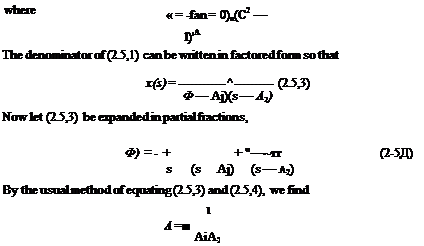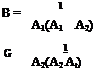where N(s) and D(s) are polynomials, and the degree of D(s) is higher than that of N(s). Let the roots of the characteristic equation D(s) = 0 be ar, so that

D(s) = (s – aq)(s – a2) ■ ■ ■ (s – an)

Then the inverse of the transform is

The effect of the factor (s — ar) in the numerator is to cancel out the same factor of the denominator. The substitution s = ar is then made in the reduced expression.

In applying this theorem to (2.5,3), we have the three roots al = 0, a2 = ^i> «з = ^21 and N(s) = 1. With these roots, (2.5,5) follows immediately from (2.5,6).