Numerical Formulation Linearized Euler Equations

A two-dimensional cascade of blades vibrating sinusoidally with a small amplitude, common angular frequency, cj, and common inter-blade phase – angle, a, may be modeled within engineering accuracy by the linearized Euler equations if the fbw remains attached along the airfoil.

The two-dimensional Euler equations in conservative form for an arbitrary control volume may be written as:

(1)

where U is the vector of conservative variables, f and g the inviscid fbxes, ft the fbw domain, E its boundary, dA the differential area pointing outward to the boundary and V the velocity of the boundary. Now we may decomposed the fbw into two parts: a steady or mean background fbw, plus a small but

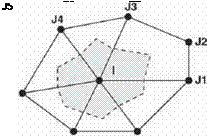
Figure I. Typical hybrid-cell grid and associated dual mesh

periodic unsteady perturbation, which in turn may be expressed as a Fourier series in time. If we retain just the first harmonic any variable may be expressed as:

U(x. t) = Uq(x) + Re(u(x)e, u’!’) (2)

where Uo represents the background flbw and u is the complex perturbation. The Euler equations may then be linearized about the mean fbw to obtain:

(——Ь ioj) I xidQ +

Jn

ioj I Uo dtf +

Jn

which is a linear equation of complex coefficients and where the first term is an additional time-derivative added to solve the equations marching in the pseudo-time r.

Spatial Discretization

The code known as Mu2s~T — L solves the two-dimensional linearized Euler equations (3) in conservative form. The spatial discretization is ob­tained linearizing the discretized equations of the non-linear version of the code Mu2s2T (Corral and Gisbert, 2002), from which the background solu­tion is obtained. The spatial domain is discretized using hybrid unstructured grids that may contain cells with an arbitrary number of faces and the solution vector is stored at the vertexes of the cells. The code uses an edge-based data structure, a typical grid is discretized by connecting the median dual of the cells surrounding an internal node (Figure 1). For the node і the semi-discrete form of Eq 3. can be written as
where Sij is the area associated to the edge ij, and nedges the number of edges that surround node j. The resulting numerical scheme is cell-centered in the dual mesh and second-order accurate. It may be shown that for triangular grids the scheme is equivalent to a cell vertex finite volume scheme. A blend of second and fourth order artificial dissipation terms, D^, is added to capture shock waves and prevent the appearance of high frequency modes in smooth fbw regions respectively. The second order terms are activated in the vicinity of shock waves by means of a pressure-based sensor and locally the scheme reverts to first order in these regions. The artificial dissipation terms can be written as

bij = IAij I Sij fif (uj – ui) – (Lj ~ Li)] (5)

where /jy^ and are the average of the artificial viscosity coefficients in the nodes і and j, L is a pseudo-Laplacian operator:

where the last approximation is only valid in regular grids and | Aij | is a 4 x 4 matrix that plays the role of a scaling factor. If |A^ | = (|u| + c)ij I, where I is the identity matrix, the standard scalar formulation of the numerical dissi­pation terms (Jameson et al., 1981) is recovered. When Aij is chosen as the Roe matrix (1981) the matricial form of the artificial viscosity (Swanson and Turkel, 1992) is obtained. The scalar version of the numerical diffusion terms has been used in this work since for the Mach numbers of interest in this work the differences between both approaches are negligible (Corral et al. 2000).

The exact, 2D, unsteady, non-refbcting boundary conditions (Giles, 1990) have been used at the inlet and outlet while the phase-shifted boundary con­ditions at the periodic boundaries are written in Fourier space as u{x, y + pitch) = u(x, y)ela.

A more detailed description of the code as well as some validation examples may be found in Corral et al. (2003)