ONE-SIDED LAPLACE TRANSFORM!
The Laplace transform is a major conceptual and analytical tool of system theory, and hence we explore its properties in more detail below. Table 2.3 lists the Laplace transforms of a number of commonly occurring functions. It should be noted that (i) the value of the function for t < 0 is not relevant to x(s) and (ii) that the integral (2.3,7) may diverge for some x(t) in combination with some values of s, in which case x(s) does not exist. This restriction is weak, and excludes few cases of interest to engineers, (iii) When the function is zero for t < 0, the Fourier transform is obtained from the Laplace transform by replacing s by ia>.
TRANSFORMS OF DERIVATIVES
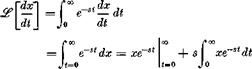 |
Given the function x(t), the transforms of its derivatives can be found from (2.3,7).
When xe~st —> 0 as t —>• oo (only this case is considered), then
= -*(0) + Ще) (2.3,14)
where x(0) is the value of x(t) when f = 0.J The process may be repeated to find the higher derivatives by replacing x(t) in (2.3,14) by x(t), and so on. The result is
f In the two-sided Laplace transform, the lower limit of the integral is — со instead of zero.
J To avoid ambiguity when dealing with step functions, t = 0 should always be interpreted as t = 0+.











