PARAMETRIC UNCERTAINTIES

• Assume as an example that the parametric uncertainties <5* enter in an affine way the state-space equations of the plant’:

x = (Ao + ^ Аі8і)х + (Bo + Bi5i)u

І І

У = (0) + £едя + (А> + £ВДг* (1.13)

І І

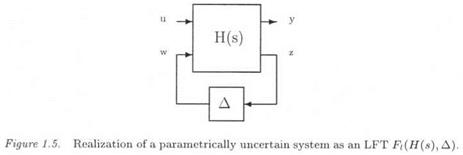
Si Є [—1,1] represents the normalized variation of the ith uncertain para­meter. Using Morton’s method (Morton and McAfoos, 1985; Morton, 1985) (see chapter 3), the uncertain plant can be transformed into an LFT у = Fi(H(s),A)u, where и and у are the physical inputs and out­puts of the plant (see equation (1.13) and Figure 1.5). Ais a diagonal matrix of the form:

The scalar Si is consequently repeated q, times, where qi is the rank of the augmented matrix Pf.

(1.15)

The idea is thus to add fictitious inputs and outputs го and z, so as to introduce then the uncertainties as an internal feedback w = Az (see Figure 1.5).

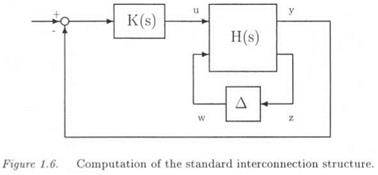
the LFT model of the uncertain plant. It suffices to connect the plant inputs and outputs u and y (see Figure 1.5) with the inputs and outputs of a controller K(s) (see Figure 1.6) to obtain the standard interconnection structure of Figure 1.1. M(s) corresponds in Figure 1.6 to the transfer matrix, which is seen by the model perturbation A, i. e. to the transfer between ги and z. Note finally that Д is no more a dynamic transfer matrix, unlike in the previous subsections. It is just a matrix gain containing real parametric uncertainties.