PHYSICAL PROPERTIES OF FLUIDS

The temperature at the freezing point of water (where T = 0 C) is T = 273.15 K, and at the boiling point under sea-level pressure, = 100° C, or = 373.15° K.

Dynamic Pressure. The mass density of air is essentially

?(kg/m ) = p(N/m )/‘R’T(°K) (19)

where ‘R’ = gas constant := 8314/29 = 290 (N-m/kg – K), up to some 90 km altitude, in one of its many definitions. In standard sea-level air, it happens to be that

pc=g/8 = 1.225 (kg/m3) (20)

2_

as listed above. The dynamic pressure q = 0.5 ^ V at sea level is accordingly

qo = (V, m/s) /2.45 = (V, kts)2/9.3

in (N/M ) or (kg/m-s2) (21)

/

/ tQOpOC-

DYNAMIC PRESSURE

q = 0.5 <jQ V2e IN (N/m2) OR (kg-m/s o= 1.225 kg/m2

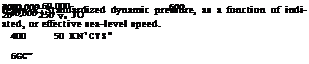Яць/ft2) = 4(N/m2)/4

I – GENERAL INFORMATION

-■**

This pressure is plotted in figure 3. Of course, there is some variation between the seasons of the year. As we all know, temperature at the ground may be 15 C lower during a winter day, and 15 ° C higher on a summer day. Atmospheric density may thus be 5% higher or lower. Also considering a possible variation of the barometric pressure in the order of + or -3%, the total variation of density and dynamic pressure at sea level as in figure 3, could be + or — 8%.

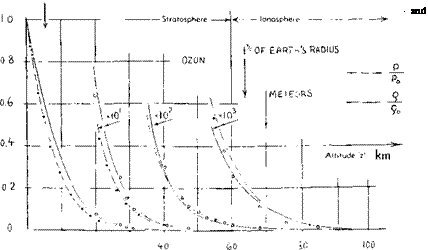
Function of Altitude. Aviation is not confined to sea – level operation. In fact, modern airliners cruise at altitudes around 10 km, not to mention the supersonic transporter SST which will do it at some 20 km. Values of tempera­ture and density ratios, standardized for the temperate zones of the earth, are plotted in figures 4 and 5. It is seen how temperature reaches a value assumed to be constant, at Z = 11 km. Density at this altitude is down to about 30% of that at sea level, which could be said to mean that the drag of an airliner be reduced to the same 30%. What is said above regarding temperature and densi ty deviations from the average or standard values at sea level, does not mean, however, that the same differentials would also be found at altitude (11 ,f)^ let alone higher altitudes, that is above some 30 km. It is also not correct to assume that the same differences as at sea level, between the equator and the poles of the earth, would also prevail at those altitudes. In fact, temperatures can be warmer at times and locations where they are expected to be colder, and vice versa.

Viscosity of the Air. The dynamic or physical or absolute viscosity in standard sea-level air is

yU0 = 1.79/105 (m2/s) (22)

for all practical purposes covered in this book, this type of viscosity is independent of pressure. As plotted in chapter I of “Fluid-Dynamic Drag”, it increases with temperature, however. For subsonic speeds (that is, be­tween T = 170 and 500 K) the viscosity of air varies in good approximation, as

o. l Ь

M ~ T (23)

By combination with the density, the kinematic viscosity vr=/^/(> is obtained (in mz/s). Under standard sea-level conditions (see tabulation above) the non-dimensional Reynolds number is then approximately

R, = VJUV V. noof (24)

where V is a suitable length such as the mean aerodynamic wing chord in particular. Of course, at altitude, the abso­lute viscosity has to be reduced as per equation (23), while the density reduces as in figure 4. For example, as Z above 11 km,

1 -9

o.7<=>

F = (0.75) Ao = 0.805 (25)

Considering the density at 11 km to be 30% of that at sea level, we obtain a kinematic viscosity

f = (0.805/0.30>£=2.7v£

for that particular altitude. The important result is that the Reynolds number R^ /vT/7‘, reduces considerably with altitude for a given airplane when flying at the same speed, that is to 1/2.7 = 37%, for example at 11 km. When flying at the same dynamic pressure (which means essen­tially at the same lift, drag and thrust) the speed at 11 km is increased to (1/ 0.3 ) = 1.8 times that at sea level. The Reynolds number is then (1.8/2.7) = 0.67 times that at sea level.

The Speed of Sound is generally

‘a’ = Vdp/d^ = Vk ‘R’ T (26)

where k = c/c =1.4= constant in atmospheric air up to some 100 km, and ‘R’ = gas constant as above. For stand­ard sea-level temperature, the sonic velocity is

‘a’ ^ 340 (m/s) ^ 660 knots (27)

Throughout the troposphere, the speed of sound reduces according to

‘a’ = 20/т7°К) in (m/s) (28)

Disregarding a tiny /decrease of g = acceleration due to gravity, the standardized speed of sound remains constant above Z = 11 km, see figure 5:

‘a’ = 0.867 X = 0.867 (340.3) = 297 (m/s)

For practical purposes, we might memorize this speed to be 1% less than = 300 m/s.

(14) Intensity and characteristics of rain, fog, icing:

a) Brim, Impingement of Water Droplets on 65-208, 65-212, 65AO(04 to 12)% Airfoils at oi = 4P, NACA TN 2952 and 3047 (1953).

b) Brun and Dorsch, On Bodies, NACA TN 2903, 3099, 3147, 3153, 3410 (1953/55).

c) Kriebel and Lundberg, Drag in Particle-Laden Gas Flow, 4 Rpts (1962) for Defense Atomic Supply Agency by Stanford Res Institute; AD-291,178.

d) Shifrin, Microstructure of Fog, NASA Trans TT F-317 (1964).

e) Preston, Ice Formation and Airplane Performance NACA TN 1598 (1948).

f) Gray, Aerodynamic Penalties by Ice on Airfoils, NASA TN D-2166 (1964).

Humidity. The amount of water “solved” in atmospheric air is usually small (less than 1% by weight, before va­porizing). Since vapor is lighter than air, the density is reduced (14,f). For example, in standard sea-level condi­tion, 100% vapor humidity reduces density by 0.6%. Hu­midity has other effects upon the air, such as upon tem­perature as a function of altitude. More dramatic results are fog, clouds, rain, snow and icing.

Fog. As stated in (14,d) fog particles are between 4 and 15 microns in diameter; and there are at least 50 droplets in one cm3. The mass ratio is then found to be in the order of 2/10 , which is negligibly small. However, fog reduces visibility to such a degree that even automobiles get into serious accidents.

Rain. Modern airplanes are designed to operate in a com­mon rate of rainfall. As reported in (14,a, b) most rain drops are in the 0.5 to 1.0 mm size range. Their average falling velocity is estimated (see chapter III of “Fluid – Dynamic Drag”) to be in the order of 4 m/s relative to the air, which is 2% of 400 knots of airplane speed, for example. A usual rainfall is said to accumulate between 1 and 2 mm per hour at the ground. The mass content of water in air is then in the order of 1/10^. In “heavy rain”, this content may be tenfold (1 per 1000), and in a cloudburst 100-fold, making the mass ratio equal to 1%. Really small drops would likely be more or less directed by the airflow around a wing, while typical rain drops may directly impact upon the upper and the frontal areas. Consequences are as follows:

a) Due to water adhering to the surface, the increase of the weight of an airplane is estimated to be a small fraction of 1%.

b) The vertical mass flow of droplets possible impinging upon the wing from above, during a “heavy” rain, might be

Figure 5. Standardized variation of temperature and Mach num­ber, up to 100 km of altitude, presented in the form of ratios.

(dm/dt) = wpa /1000 (kg/m2 s) (29)

where m = mass per unit wing area and (1/1000) as above. For the velocity w = 4 m/s, and an air density pa =

1 kg/m, the impact pressure of the rain drops might then be

(dm/dt) w g = 16(9.81 >/1000 « 0.16 (kg-s/m* ) = (N/m2)

By comparison, the mass loading of an airplane is between 150 and 300 kg/m2 or a v/eight loading of 1500 to 3000 N/m 2 (or 35 to 70 lb/ft ). The impact of rain considered, would thus not be of any importance.

c) In regard to drag, rain drops will more or less impinge upon the frontal area of an airplane. This type can thus be treated as a free-particle flow (similar to the Newtonian type as described in “Fluid-Dynamic Drag”).

Assuming that the rain drops captured by the frontal area S, of an airplane, lose half of their momentum (that they are accelerated to lA the airplane’s speed V) we obtain

iD = 0.5 V2^S. (mw/ma) (kg-m/s21) = N

(30)

where “w” indicates water and “a” = air. Assuming an effective (capturing) frontal area ratio S./S = 0.1, the incremental drag coefficient may then be

AC0 = (SjS)(fJfa) (nv/ma) (31)

For a constant (mцг/nu) = 0.1%, as in “heavy rain”, the result is ДС0= 0.08. This would be as much as the air­plane’s original drag at CL = 1. According to (14,c) it seems, however, that a portion of the rain drops larger than assumed above, is diverted by the air flow around the wing, for example.

Icing. The formation (deposit) of ice upon the frontal areas of an airplane (such as the leading edge around the stagnation line) can increase weight and drag appreciably. At cruising speed, drag increments up to 80% are reported in (14,e), while the propeller efficiency may be reduced 10 or even 20%.

Wind profiles (velocity w or dynamic pressure as a function of altitude Z above ground) are plotted in chap­ter IV of “Fluid-Dynamic Drag”, up to altitudes Z be­tween 25 and 250 m. Similar data are reported in (15,a). It appears that in properly developed steady wind over a plane unobstructed surface (such as an airfield) the varia­tion is approximately

i/n ’ г/г

w,/w, =(Zz/Z,) ; or q^/qor, =(Z2/Z,) (32)

where n between 6 and 8. At “higher” Reynolds numbers, distributions within turbulent boundary layers usually correspond to w ^ Z/? . Behind obstacles (such as build­ings at the edge of an airport) there is a deficiency of speed. As shown in (15 ,b) a gradient much stronger than that indicated by n = 6 or 8, may then be found above the level of those obstructions. Regarding the climb-out per­formance of airplanes, any positive gradient will help. It seems, however, that when landing into a strong wind (and possibly over an obstacle) the negative gradient can be dangerous. While reducing the airplane speed, thus increasing the lift coefficient, the wind velocity also re­duces, thus possibly leading to wing stalling at angles of attack beyond that for C^x. Airplanes are thus operated at lift coefficients approximately 70% of the maximum to allow for turbulent velocity conditions and control inputs.

(B) Physical Properties of Water

There are “lifting” devices used in water such as rudders and hydrofoils. Properties of water are presented in “Fluid-Dynamic Drag”. They are here given again, in met­ric units.

The Compressibility of water dy/dp, measured in (kg/m3 )/(N/m2) = (kg/mN) = (s/m)2 , is very small in comparison to that in air. As a consequence, the speed of sound ‘a’ = t/dp/dp is in the order of 1440 m/s (4700 ft/sec, 2800 kts) in comparison to 340 m/s (1117 ft/sec, 660 kts), in sea-level air. For example, it takes more than 7 hours for an explosion, say at the coast of Japan, to be “heard” in San Francisco (over a distance of almost 5000 sea miles, or 9000 km). It would only be less than 2 hours, however, to detect the same disturbance by sonar. For comparison, the travel time is in the order of 10 hours by subsonic jet airplane (if non-stop at M = 0.8), and less than 3 hours by Supersonic Transport (at 2000 mph, approaching M = 3).

Dynamic Pressure. The density of sea water is some 840 times that of sea-level air. For all practical purposes, this density can be considered to be constant (to be inde­pendent of temperature and pressure):

p (fresh water) = 1000 kg/m3

In average (Atlantic) sea water, with a salinity in the order of 3.5% (16,c), the density is higher:

p (sea water) = 1025 kg/m3 2.0 lb-sec/ft Corresponding to these densities, the dynamic pressure is

q = 500 g V2 in (N/m2) or (kg/m-s2)	in fresh water	(33)
q = 513 g V2 in (N/m2) or (kg/m-s2)	in sea water	(34)
Using у as above, we also obtain conveniently:
q = 500 (V m/sf in (kp/m2)	in fresh water	(35)
* q = (V, ft/sec)2 in (lb/ft2)	in sea water	(36)
q = 0.97(V2) in (lb/ft2)	in fresh water	(37)
Equation (37) is plotted in figure 6	in fresh water	ex-

pecting that the metric system will be accepted last, in the field of naval architecture.

(15) Characteristics of atmospheric wind:

a) Lettau, “Exploring Atmosphere’s First Mile”, Pergamon 1957; also “Wind” in chapter 5 of “Handbook of Geo­physics”, MacMillan 1960.

b) Stearns, “Atmospheric Boundary Layer”, Univ Wisconsin (1964); AD-611, 209.

c) Am Meteorological Soc, Wind for Aerospace Vehicles, Bull 11 (1964) p 720.

The Viscosity of water, needed for the computation of the Reynolds number, is plotted in chapter I of “Fluid – Dynamic Drag”, in the form of V At the standard temperature of 15 C, the kinematic viscosity is between (1.16 in fresh and 1.13 in sea water)/ К)5 (ft* /sec), which is between (1.08 and 1.05)/106 (m2/s). Contrary to that in air, this viscosity reduces as temperature is increased, that is roughly as

S =M/ f’-l/T6 (38)

Water Tunnels (17). The high density of water makes it possible to obtain high Reynolds numbers in a tunnel built in the same form as that of an ordinary wind tunnel. For example, in a comparatively large, but low-speed wind tunnel we may have:

c =	1	m	wing chord
V =	40	m/s	air speed
q =	100	kp/nZ	dynamic pressure
Rc =	2.8	(10)6	Reynolds number

For operational reasons, the size of a water tunnel might be restricted. We could obtain the following, however:

c –	0.5	m	wing chord
V =	10	m/s	water speed
q =	50000	kp/m2	dynamic pressure
R =	4.3	(10)6	Reynolds number

As in equation (38) the viscosity of water reduces as temperature is increased. Therefore, when increasing the absolute temperature from the standard 288° К to 316 K, that is from 15^ C to 43 C (which is only 4 C more than our blood temperature) the Reynolds number in the water tunnel suggested, can be doubled. A number Rc approaching 107 could thus be obtained. For many pur­poses, we just do not need such high R’numbers; and at a speed, say of 2 m/s the most instructive flow patterns could easily be produced in water by adding a suitable substance. To make the water tunnel still more attractive, its low power requirement is mentioned. For a one meter squared test cross section, the power is approximately

power = 0.5 q 0.25 ^ V3/1000 = V3/4 kwatt

For V = 10 m/s, that would be 250 kwatt; and for 2 m/s, only 2 kwatt. [6] [7] [8]

Cavitation is vaporization (boiling) due to reduced pres­sure. Fundamentals and examples of cavitation are pre­sented in chapter X of “Fluid-Dynamic Drag”. Really pure water (distilled, in a pure container) may not cavitate at all. However, all kinds: of microscopic impurities (such as cosmic dust, particles remaining in drinking water after filtering, tiny air bubbles in the interface of sea water, or plankton) will “always” provide the nuclei needed to start a vapor bubble. The critical pressure at which water at a temperature of 15 C begins to turn into gas (vapor) is less than 0.016 of the atmospheric pressure (= 33 lb/ft2 = 1600 N/m2). So, for practical purposes, we may as well say the vapor pressure p^ is zero.

The Cavitation Number indicates the tendency of the ambient flow to cavitate, when meeting an obstacle:

where q = dynamic pressure, and pa = ambient pressure. At standard sea-level pressure (“at” the surface of open sea water) the coefficient of that pressure (pa – p„) = 2116- 33 = 2083 lb/ft2, is

<ґ – (p – pj/q = 2090/(V, ft/sec)2 = 195/(V, m/sf

(40)

For each unit of submergence “h” (below the free water surface) we have to add a

2

д p/q = 64 lb/ft for each foot of sea water

д p/q = 1000 kp/m2 for each meter of fresh water