THE CASE OF A SINGLE BLOCK OF NEGLECTED DYNAMICS

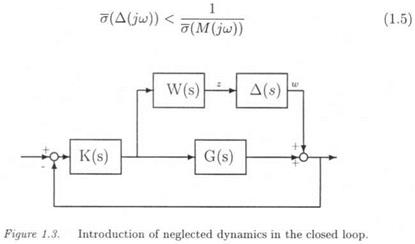
• A single block of neglected dynamics A(s) is introduced in the closed loop. Consider the example of Figure 1.3: the plant model G(s), the controller K(s) and the weighting function W(s) are known transfer matrices, while the normalized neglected dynamics A(s) correspond to an uncertain transfer matrix, which is just known to satisfy the inequality:

By definition of the Hoo norm, this relation becomes at frequency ш:

°{A(juj)) < 1 (1.4)

As a first point, the model uncertainty Д(з) is said to be additive in the context of Figure 1.3, since the true plant is modeled as (?(s)+A(s)W(s). This additive representation of the model uncertainties is especially used in the context of flexible structures, to represent an uncertainty in the bending modes dynamics. As a second point, the true uncertainty in the plant dynamics is A(s)VF(s), so that the weighting function W(s) is used to introduce our knowledge of this uncertainty in the plant dynamics (see below). [2]

• Assume that the nominal closed loop (i. e. the one corresponding to A(s) = 0) is asymptotically stable. The issue is to determine the max­imal amount of neglected dynamics, for which the closed loop remains stable. A simple solution is provided by the small gain theorem, which gives a necessary and sufficient condition of stability of the closed loop at frequency w:

As expected, if the normalized neglected dynamics A(s) satisfy equa­tion (1.4), the model uncertainty which is induced by the

reduction of the plant model, satisfies inequality (1.6).