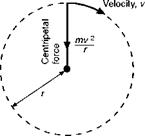
Centripetal force and centripetal acceleration
We all know the direction of the force as a result of practical experience. Swing a stone round on the end of a piece of string. In what direction does the string pull on the stone to keep it on its circular path? Why, towards the centre of the circle, of course, and since force and acceleration are in the same direction, the acceleration must also be towards the centre.
We know too that the greater the velocity of the stone, and the smaller the radius of the circle on which it travels, the greater is the pull in the string, and therefore the greater the acceleration. The acceleration is actually given by the simple formula v2lr, where v is the velocity of the body and r the radius of the circle.
The force towards the centre is called centripetal force (centre-seeking force), and will be equal to the mass of the body X the centripetal acceleration, i. e. to m X v2lr (Fig. 1.4).
We have made no attempt to prove that the acceleration is v2lr – the proof will be found in any textbook on mechanics – but since it is not easy to conceive of an acceleration towards the centre as so many metres per second per second when the body never gets any nearer to the centre, it may help if we
|
Direction of rotation — – v
|
Fig 1.4 Centripetal force
translate the algebraic expression into some actual figures. Taking the simple example of a stone on the end of a piece of string, if the stone is whirled round so as to make one revolution per second, and the length of the string is 1 metre, the distance travelled by the stone per second will be 2ттr, i. e. 2-тт X 1 or 6.28 m. Therefore
v = 6.28 m/s, r = 1 m
.’. acceleration towards centre = v2lr
= (6.28 X 6.28)/l = 39.5 m/s2 (approx)
Notice that this is nearly four times the acceleration of gravity, or nearly 4g. Since we are only using this example as an illustration of principles, let us simplify matters by assuming that the answer is 4g, i. e. 39.24 m/s2.
This means that the velocity of the stone towards the centre is changing at a rate 4 times as great as that of a falling body. Yet it never gets any nearer to the centre! No, but what would have happened to the stone if it had not been attached to the string? It would have obeyed the tendency to go straight on, and in so doing would have departed farther and farther from the centre.
What centripetal force will be required to produce this acceleration of 4g? The mass of the stone X 4g.
So, if the mass is 1/2 kg, the centripetal force will be 1/2 X 4g = 2 X 9.81 = 19.62, say 20 newtons.
Therefore the pull in the string is 20 N in order to give the mass of 1/2 kg an acceleration of 4g.
Notice that the force is 20 newtons, the acceleration is 4 g. There is a horrible tendency to talk about ‘g’ as if it were a force; it is not, it is an acceleration.
Now this is all very easy provided the centripetal force is the only force acting upon the mass of the stone. However, in reality there must be a force of gravity acting upon it.
If the stone is rotating in a horizontal circle its weight will act at right angles to the pull in the string, and so will not affect the centripetal force. But of course a stone cannot rotate in a horizontal circle, with the string also horizontal, unless there is something to support it. So let us imagine the mass to be on a table – but it will have to be a smooth, frictionless table or we shall introduce yet more forces. We now have the simple state of affairs illustrated in Fig. 1.5.
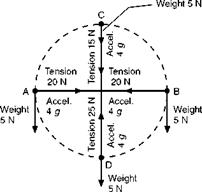
Now suppose that we rotate the stone in a vertical circle, like an aeroplane looping the loop, the situation is rather different (Fig. 1.6). Even if the stone were not rotating, but just hanging on the end of the string, there would be a tension in the string, due to its weight, and this as near as matters would be very roughly 5 newtons, for a mass of 1/2 kg. If it must rotate with an acceleration of 4g the string must also provide a centripetal force of 20 newtons. So when the stone is at the bottom of the circle, D, the total pull in the string will be 25 N. When the stone is in the top position, C, its own weight will act towards the centre and this will provide 5 N, so the string need only pull with an additional 15 N to produce the total of 20 N for the acceleration of 4g. At the side positions, A and B, the weight of the stone acts at right angles to the string and the pull in the string will be 20 N.
To sum up: the pull in the string varies between 15 N and 25 N, but the acceleration is all the time 4g and, of course, the centripetal force is all the time —20 N. From the practical point of view, what matters most is the pull in the string, which is obviously most likely to break when the stone is in position D and the tension is at the maximum value of 25 N.
To complicate the issue somewhat, suppose the stone rotates in a horizontal circle, but relies on the pull of the string to hold it up (Fig. 1.7), and that the string has been lengthened so that the radius on which the stone is rotating is
Direction of rotation
Fig 1.5 Stone rotating in a horizontal circle, supported on a table
|
Direction of rotation
|
Fig 1.6 Stone rotating in a vertical circle
still 1 metre. The string cannot of course be horizontal since the pull in it must do two things – support the weight of the stone and provide the centripetal force.
Here we must introduce a new principle.
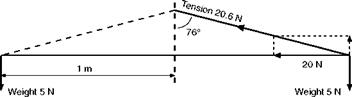
A force of 5 N, vertically, is required to support the weight.
A force of 20 N, horizontally, is required to provide the centripetal force. Now five plus twenty does not always make twenty-five! It does not in this example, and for the simple reason that they are not pulling in the same direction. We must therefore represent them by vectors (Fig. 1.7), and the diagonal will represent the total force which, by Pythagoras’ Theorem, will be
V(202 + 52) = V425 = 20.6 N
The tangent of the angle of the string to the vertical will be 20/5 = 4.0. So the angle will be approx 76°. Expressing the angle, 0, in symbols –
Centripetal force
tan 0 = . = (m X v2/r)IW
Weight
|
= (m X v2lr)lmg
|
Fig 1.7 Stone rotating in a horizontal circle, with string support
(mg being the weight expressed in newtons)
= v[1]lrg
This angle 0 represents the correct angle of bank for any vehicle, whether it be bicycle, car or aeroplane, to turn a corner of radius r metres, at velocity v metres per second, if there is to be no tendency to slip inwards or to skid outwards.