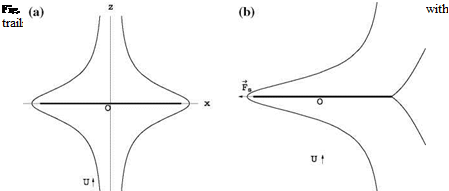
Circular Arc

For this case, e = 0 and 8 > 0. The polar coordinates are centered at (0, 8). The potential function reads

Ф = 2Ua’ cos(0 — a) — (в — a)

where a’2 = a2 + 82. The azimuthal component of velocity on the cylinder is

The circulation, that places the stagnation point at (0, a) is

Г — 4n U (a sin a + 8 cos a) (2.101)

and the lift coefficient as given by the Kutta-Joukowski lift theorem

The most interesting situation for this airfoil corresponds to a = 0 where a symmetry w. r.t. the z-axis (and Z-axis) is obtained. In this case, the surface velocity reduces to a simple expression

V _ a2 + 28 sin ву/a2 + (8 sin в)2 (2103)

— 2 2 (2.103)

U a2 + 82

The pressure coefficients are shown in Fig. 2.27 for a — 0, d — 0.1 and C — 0.2.

A consequence of symmetry is that the leading edge, as the trailing edge, satisfies a Kutta-Joukowski condition. This is only possible for a — 0. The leading edge is “adapted”. a — 0 is the ideal angle of attack for the circular arc. The lift coefficient in this case is Cl — 2n 8. The lift per unit span

L’ — 4npU 28 — 2npU 2d

(a) (b)

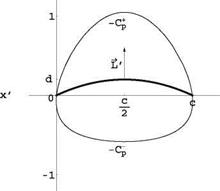—Cp — Cp

only depends on d, where d = 28 represents the height of the circular arc in the physical plane (the chord is c = 4a). This result was first obtained by Kutta in 1902. The center of pressure is at the center of the arc, i. e.

(2.105)