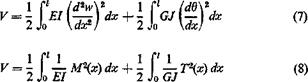ELEMENTARY BEAM THEORY

Consider a cylindrical beam of uniform isotropic material. In each cross section of the beam, two mutually perpendicular principal axes, passing through the centroid of the cross section, can be determined, about which the second moments (the moments of inertia) of the beam cross-sectional area assume stationary values with respect to rotation of the centroidal axes, and the product of inertia of the area vanishes. The plane containing one of the principal axes of all cross sections is called a
principal plane. If the beam is acted on by a bending moment M in a principal plane, the beam will deflect in that plane. Let 1 /R represent the change of curvature of the beam in that plane; then, within the elastic limit of the beam,

R~ El

where E is Young’s modulus of the material, and I is the moment of inertia* of the beam cross section about a principal axis perpendicular to the principal plane in which M acts. Let у denote the distance from the neutral plane; then the bending stress is given by

Equations 1 and 2 are applicable, approximately, also to a straight beam with nonuniform cross sections subjected to distributed external loads, provided that E, I, 1 /R, and M are the local values and that the variation of the beam cross section is gradual. They are, however, not directly applicable to curved beams.

Equations 1 and 2 are derived under the assumptions that the displace­ment of the beam is small, that the Hooke’s law between stress and strain holds, and that the plane cross sections of the beam remain plane during deformation. They are referred to as engineering beam formulas.

When a system of external forces acts on a beam, it produces shear and bending moment in the beam. The loading (lateral force per unit length) p, the shear S, and the moment M are connected by the equations

where x denotes distance measured along the axis of the beam. For a given beam, after a given direction has been chosen for the coordinate x, the signs (i. e., the positive senses) of p, S, and M may be consistently chosen by verifying Eqs. 3.

If a twisting moment whose vector is parallel to the beam axis is applied on the beam, the cross sections will rotate about the beam elastic axis.

* For semimonocoque thin-walled box beams part of the skin may be buckled under a compressive stress. The contribution of such buckled panels to the bending stiffness can be accounted for by reducing the actual width of the skin panels to their "effective width.” In this case the factor / in Eq. 1 is the "effective” moment of inertia, computed on the basis of the effective width of skin.1-3

The rate of change of the angle of twist в (radians) along the length of the beam is given by the formula

d6_T_ dx ~ GJ

where T is the twisting moment about the shear center of a section at x, and GJ denotes the torsional rigidity. G is the shear modulus of rigidity, but У stands for the quantities as shown in Table 1.1, according to various cross sections.1-27

In Eq. 4, the positive sense of the vector 0 is chosen as that of the co­ordinate axis x. However, the positive sense of the torque T, like that of the shearing stresses, cannot be determined until the positive side of the surface on which the torque acts has been chosen. The sign convention is as follows: Consider a beam element of length dx, which is bounded on both ends by normal cross sections of the beam. Let normal vectors of the cross sections be drawn from inside of the element, (the so-called outer normals). If a torque T acting on the end of the beam element agrees in its vector sense with that of the outer normal, then Г is positive; otherwise it is negative.

If the beam is subjected to a system of distributed twisting moment of intensity m per unit length, then the twisting moment T is variable across the span. Let us define m as positive if its vector sense agrees with that of x, which we shall assume to be pointing to the right. Then on an element of length dx, there acts a torque — T on the left-hand side, a torque T + dT on‘the right-hand side, and a torque m dx on the element. (See Fig 1.21 on p. 48.) Thus the condition of equilibrium of the element demands that

— T + m dx + T dT = 0 or

Combining Eqs. 4 and 5, we obtain the following relation for a beam subjected to a system of distributed twisting moments:

In engineering beam theory, the beam deflection is assumed to be infinitesimal. Let w be the deflection of the beam; then, approximately,

1 d2w M ~R ~ dx2 ~ ~El

Table 1.1
Beam Cross Section
Circular cylinder	Polar moment of inertia = — (t/1 — rf,4)
Aa2b2 4(й2 + Ь2У
T Elliptic cylinder
A« 40TP (aPProx-)
Ip = polar moment of inertia about centroid
Rectangular section
T
A? ‘з ’
A = area of cross section
Я
Single-bay thin – walled tube
A — area enclosed by tube walls
^ Гд2(Иі2 аіг(^і ^г)2 ~Ь ДрИг L йоійіг + йігвго + агоат
Double-bay thin – walled tube
where aiS —	the integral being taken
along boundary between A{ and A}.

When a positive sense is chosen for w, the positive sense of M must be checked against Eq. 6. Such a check of signs should always be made in order to avoid confusion in the calculations.

From Eqs. 3 and 6, we obtain

where w is the deflection and p is the loading per-unit length acting on the beam. The positive senses of w and p agree with each other.

When the external forces acting on the beam do not lie in a principal plane, the forces should be resolved into components lying in each of the two principal planes. The deflection of the beam can then be computed in these two planes separately and then added vectorially. Similarly, if an external couple acting on the beam is inclined to the beam axis, the couple should be resolved into a bending moment and a twisting moment, and the induced displacements computed separately.

In solid beams, the deflection is essentially induced by the bending moments. The deflection caused by the shear 8 can be neglected. But in thin-walled box beams the shear deflection can become quite important, particularly in calculating the higher-order vibration frequencies and modes.184

Accompanying the application of external load on the beam, elastic strain energy is stored in the beam. For a solid beam the strain energy due to transverse shear stresses is usually negligible in comparison with that due to bending and torsion. If the deflection w(x) and the torque T(x) are measured at the shear center of a section at x, then the strain energy can be written as

where l is the length of the beam. For thin-walled structures, the strain energy due to transverse shear is not negligible. A term of the following form,

V=l-[ K{x)Sx)dx (9)

2 Jo

should be added, where K(x) is a function of the cross-sectional shape and the material of the structure.

The elementary theories of torsion and bending are based on assump­tions that are usually violated in actual aircraft wing structures. The elementary torsion theory is valid for a shell of constant cross section, subjected to a torque at each end in the form of a shear flow that is distributed in the section in accordance with the theory, and that leaves the end sections free to warp out of their original planes. An actual wing has a variable section and is subjected to distributed torque loads; as a result, the tendency to warp, in general, differs from section to section, and secondary stresses are set up by the resulting interference effects. The normal stresses so induced are called the “bending stresses due to torsion.” Similarly, the elementary bending theory is strictly valid if the applied load is a pure bending moment. In actual wing structures, the bending moments are produced by transverse loads, and, in general, the shear strains in the beam produced by these loads violate the assumption that plane cross sections remain plane. As in the torsion case, inter­ference effects between adjacent sections may produce secondary stresses. In the particular case of thin-walled box beams, the effect of the shear strain on the distribution of normal stresses is called the “shear lag.”

A general theory of bending and torsion of beams of variable cross sections, subject to a variable loading, is very complicated. A practical solution exists for thin-walled cylinders under the assumption that cross – sectional shape of the cylinders is maintained by diaphragms, which are infinitely rigid against deformation in their own planes but are perfectly flexible for deflection normal to their planes. For box beams of closed sections the effect of shear lag is important with respect to the stress distri­bution, but is insignificant with respect to the deflection of the beam except for swept wings. This is because the deviations of the stresses from those predicted by the elementary theories are local, and local disturbances are smoothed out by the integration process necessary to calculate deflections. The deviations of the deflections from those predicted by the elementary theories are therefore much smaller than the stress deviations. For this reason adequate accuracy can often be achieved for the deflection (and the influence-coefficient.) calculations, even when highly simplified theories are used. On the other hand, the effect of shear lag and restrained warp­ing is very large for thin-walled structures with open cross sections (the portion of a wing with a large cutout may be regarded as open sections). See articles listed in the bibliography at the end of this chapter for the treatment of special problems. See, in particular, Ref. 1.70.

In applying the results of the elementary beam theory to airplane structures, considerable engineering judgment is often necessary because the effects of cutouts, shear lag, differential bending of the spars, dis­continuous changes of section properties, etc., must be properly accounted for. Occasionally a wing or a tail cannot at all be considered as a “beam” or a “torque tube.” In such cases a more comprehensive analysis of the elastic deformation is necessary. In aeroelasticity the most convenient scheme of describing the elastic properties of a structure is to specify its influence functions. The calculation of the influence functions for a structure other than a simple beam may be very difficult, but it is a prerequisite for aeroelastic analyses.