Fluid dynamics

We will now treat a fluid that is moving so that, in addition to gravita­tional forces, inertial and shearing forces must be considered.

A typical flow around a streamlined shape is pictured in Figure 2.4. Note that this figure is labled “two-dimensional flow”; this means simply that the flow field is a function only of two coordinates (x and y, in the case of Figure 2.4) and does not depend on the third coordinate. For example, the flow of wind around a tall, cylindrical smokestack is essentially two-dimensional except near the top. Here the wind goes over as well as around the stack, and the flow is three-dimensional. As another example, Figure 2.4 might represent the flow around a long, streamlined strut such as the one that supports the wing of a high-wing airplane. The three-dimensional counterpart of this shape might be the blimp.

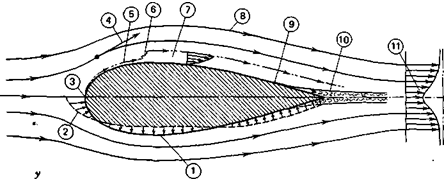Several features of flow around a body in general are noted in Figure 2.4. First, observe that the flow is illustrated by means of streamlines. A stream­line is an imaginary line characterizing the flow such that, at every point along the line, the velocity vector is tangent to the line. Thus, in two-dimensional

Figure 2.4 Two-dimensional, flow around a streamlined shape.

flow, if y(x) defines the position of a streamline, y(x) is related to the x and у components of the velocity, u(x) and v(x), by

dy _ v(x) dx u(x)

Note that the body surface itself is a streamline.

In three-dimensional flow a surface swept by streamlines is known as a stream surface. If such a surface is closed, it is known as a stream tube.

The mass flow accelerates around the body as the result of a continuous distribution of pressure exerted on the fluid by the body. An equal and opposite reaction must occur on the body. This static pressure distribution, acting everywhere normal to the body’s surface, is pictured on the lower half of the body in Figure 2.4. The small arrows represent the local static pressure, p, relative to the static pressure, po, in the fluid far removed from the body. Near the nose p is greater than p0; further aft the pressure becomes negative relative to po- If this static pressure distribution, acting normal to the surface, is known, forces on the body can be determined by integrating this pressure over its surface.

In addition to the local static pressure, shearing stresses resulting from the fluid’s viscosity also give rise to body forces. As fluid passes over a solid surface, the fluid particles immediately in contact with the surface are brought to rest. Moving away from the surface, successive layers of fluid are slowed by the shearing stresses produced by the inner layers. (The term “layers” is used only as a convenience in describing the fluid behavior. The fluid shears in a continuous manner and not in discrete layers.) The result is a thin layer of slower moving fluid, known as the bbundary layer, adjacent to the surface. Near the front of the body this layer is very thin, and the flow within it is smooth without any random or turbulent fluctuations. Here the fluid particles might be described as moving along in the layer on parallel planes, or laminae; hence the flow is referred to as laminar.

At some distance back from the nose of the body, disturbances to the flow (e. g., from surface roughnesses) are no longer damped out. These disturbances suddenly amplify, and the laminar boundary layer undergoes transition to a turbulent boundary layer. This layer is considerably thicker than the laminar one and is characterized by a mean velocity profile on which small, randomly fluctuating velocity components are superimposed. These flow regions are shown in Figure 2.4. The boundary layers are pictured considerably thicker than they actually are for purposes of illustration. For example, on the wing of an airplane flying at 1(X) m/s at low altitude, the turbulent boundary 1.0 m back from the leading edge would be only approximately 1.6 cm thick. If the layer were still laminar at this point, its thickness would be approximately 0.2 cm.

Returning to Figure 2.4, the turbulent boundary layer continues to thicken toward the rear of the body. Over this portion of the surface the fluid

is moving into a region of increasing static pressure that is tending to oppose the flow. The slower moving fluid in the boundary layer may be unable to overcome this adverse pressure gradient, so that at some point the flow actually separates from the body surface. Downstream of this separation point, reverse flow will be found along the surface with the static pressure nearly constant and equal to that at the point of separation.

At some distance downstream of the body the separated flow closes, and a wake is formed. Here, a velocity deficiency representing a momentum loss by the fluid is found near the center of the wake. This decrement of momentum (more precisely, momentum flux) is a direct measure of the body drag (i. e., the force on the body in the direction of the free-stream velocity).

The general flow pattern described thus far can vary, depending on the size and shape of the body, the magnitude of the free-stream velocity, and the properties of the fluid. Variations in these parameters can eliminate transition or separation or both.

One might reasonably assume that the forces on a body moving through a fluid depend in some way on the mass density of the fluid, p, the size of the body, l, and the body’s velocity, V. If we assume that any one force, F, is proportional to the product of these parameters each raised to an unknown power, then

F oc p°vblc

In order for the basic units of mass, length, and time to be consistent, it follows that

Considering M, L, and T in order leads to three equations for the unknown exponents a, b, and c from which it is found that a = 1, b =2, and c = 2. Hence,

F oc pv42 (2.12)

Fqr a particular force the constant of prdfc>ortionality in Equation 2.12 is referred to as a coefficient and is modified by the name of the force, for example, the lift coefficient. Thus the lift and drag forces, L and D, can be expressed as

L = l2pV2SCL (2.13 a)

D = 12pV2SCD (2.13b)

Note that the square of the characteristic length, l2, has been replaced by a reference area, S. Also, a factor of 1/2 has been introduced. This can be done, since the lift and drag coefficients, CL and CD, are arbitrary at this point. The quantity pV2/2 is referred to as the dynamic pressure, the significance of which will be – made clear shortly.

For many applications, the coefficients CL and CD remain constant for a given geometric shape over a wide range of operating conditions or body size. For example, a two-dimensional airfoil at а Г angle of attack will have a lift coefficient of approximately 0.1 for velocities from a few meters per second up to 100 m/s or more. In addition, CL will be almost independent of the size of the airfoil. However, a more rigorous application of dimensional analysis [see Buckingham’s – n theorem (Ref. 2.1)] will result in the constant of proportionality in Equation 2.12 possibly being dependent on a number of dimensionless parameters. Two of the most important of these are known as the Reynolds number, R, and the Mach number, M, defined by,

where l is a characteristic length, V is the free-stream velocity, ju, is the coefficient of viscosity, and a is the velocity of sound. The velocity of sound is the speed at which a small pressure disturbance is propagated through the fluid; at this point, it requires no further explanation. The coefficient of viscosity, however, is not as well known and will be elaborated on by reference to Figure 2.5. Here, the velocity profile is pictured in the boundary layer of a laminar, viscous flow over a surface. The viscous shearing produces a shearing stress of rw on the wall. This force per unit area is related to the gradient of the velocity u(y) at the wall by

(2.15)

Actually, Equation 2.15 is applicable to calculating the shear stresses between fluid elements and is not restricted simply to the wall. Generally, the viscous shearing stress in the fluid in any plane parallel to the flow and away

у

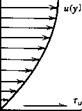ІШШШІжшшшіш Figure 2.5 Viscous flow adjacent to a surface.

from the wall is given by the product of ц and, the velocity gradient normal to the direction of flow.

The kinematic viscosity, v, is defined as the ratio of ц to p.

it

P v is defined as a matter of convenience, since it is the ratio of p. to p that governs the Reynolds number. The kinematic viscosity for the standard atmosphere is included in Figure 2.3 as an inverse fraction of the standard sea level value.

A physical significance can be given to the Reynolds number by multi­plying numerator and denominator by V and dividing by l.

QiVfl)

In the following material (see Equation,2.28) the normal pressure will be shown to be proportional to pV2 whereas, from Equation 2.15, pV/l is proportional to the shearing stress. Hence for a given flow the Reynolds number is proportional to the ratio of normal pressures (inertia forces) to viscous shearing stresses. Thus, relatively speaking, a flow is less viscous than another flow if its Reynolds number is higher than that of the second flow.

The Mach number determines to what extent fluid compressibility can be neglected’ (i. e., the variation of mass density with pressure). Current jet transports, for example, can cruise at Mach numbers up to approximately 0.8 before significant compressibility effects are encountered.

At lower Mach numbers, two flows are geometrically and dynamically similar if the Reynolds numbers are the same for both flows. Hence, for example, for a given shape, CD for a body 10 m long at 100 m/s will be the same as CD for a 100-m long body at 10 m/s. As another example, suppose transition occurs 2 m back from the leading edge of a flat plate aligned with a flow having a velocity of 50 m/s. Then, at 25 m/s transition would occur at a distance of 4 m from the leading edge. Obviously the effects of R and M on dimensionless aerodynamic coefficients must be considered when interpreting test results obtained with the use of small models.

For many cases of interest to aerodynamics the pressure field around a shape can be calculated assuming the air to be inviscid and incompressible. Small corrections can then be made to the resulting solutions to account for these “real fluid” effects. Corrections for viscosity or compressibility will be considered as needed in the following chapters.