INTEGRAL FORM OF THE FLUID DYNAMIC EQUATIONS
To develop the governing integral and differential equations describing the fluid motion, the various properties of the fluid are investigated in an arbitrary control volume that is stationary and submerged in the fluid (Fig. 1.8). These properties can be density, momentum, energy, etc., and any change with time of one of them for the fluid flowing through the control volume is the sum of the accumulation of the property in the control volume and the transfer of this property out of the control volume through its boundaries. As an example, the conservation of mass can be analyzed by observing the changes in fluid density p for the control volume (c. v.). The mass mc v within the control volume is then:
mc. v. = [ pdV (1.13)
•’C. V.
where dV is the volume element. The accumulation of mass within the control volume is
![]()
![]() (1.13a)
(1.13a)
The change in the mass within the control volume, due to the mass leaving (mout) and to the mass entering (min) through the boundaries (c. s.) is:
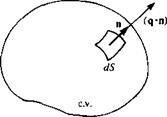 |
mOM – min = p(q • n) dS (1.14)
where q is the velocity vector (к, v, w) and pq • n is the rate of mass leaving across and normal to the surface element dS (n is the outward normal), as shown in Fig. 1.8. Since mass is conserved, and no new material is being produced, then the sum of Eq. (1.13a) and Eq. (1.14) must be equal to zero:
<ii5>
Equation (1.15) is the integral representation of the conservation of mass. It simply states that any change in the mass of the fluid in the control volume is equal to the rate of mass being transported across the control surface (c. s.) boundaries.
In a similar manner the rate of change in the momentum of the fluid flowing through the control volume at any instant d(mq)cv,/dt is the sum of the accumulation of the momentum per unit volume pq within the control volume and of the change of the momentum across the control surface boundaries:
=11. m dv+{, ‘’ч(ч • ■>dS <L l6>
This change in the momentum, as given in Eq. (1.16), according to Newton’s second law must be equal to the forces E F applied to the fluid inside the control volume:
![]() d(mq)c v „
d(mq)c v „
The forces acting on the fluid in the control volume in the xt direction are either body forces pft per unit volume, or surface forces лут, у per unit area, as discussed in Section 1.4:
(EfW pfdV+( n, TvdS (1.18)
‘ ‘ І «ЧГ. І». Jc. S.
where n is the unit normal vector that points outward from the control volume.
By substituting Eqs. (1.16) and (1.18) into Eq. (1.17), the integral form of the momentum equation in the і direction is obtained:
~ f pq, dV + f pq,(q – n)dS= [ pfidV+ f прц dS (1.19)
*c. v. ^c. s. Л:.V. *4r. s.
This approach can be used to develop additional governing equations, such as the energy equation. However, for the fluid dynamic cases that are being considered here, the mass and the momentum equations are sufficient to describe the fluid motion.











