ORDINATE-CROSSING RETURN PERIOD
With reference to Fig. 2.10, let us define an “event” as a crossing of the random curve through the strip Av at v. The time At associated with a single event that has a slope in the range Av is
During a total time T —> oo, the portion spent in the domain Av, Av of the (v, v) space is
A T = Tf(v, v) Av Av
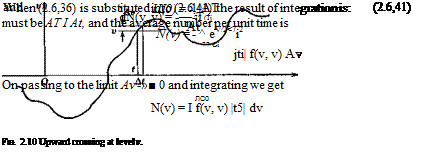 |
Hence, the total number of events with slopes in the range Av in the time T
|
v/ox |
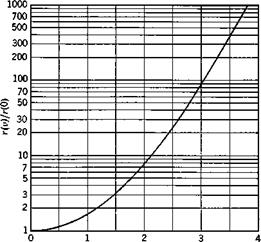
Fig. 2.11 Return period.
Since N(v) includes both upward and downward crossings, the average number of upward crossings, or “positive events” is
N+(v) = iN(v) = — ^ (2.6,43)
2ir (Tj
The average interval between positive events is called the return period.
r(v) = —— = 2тг ^ evV2^2 (2.6,44)
N+(v) a2
which is plotted in Fig. 2.11.
DISTRIBUTION OF PEAKS
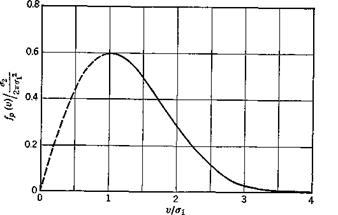
It is observed that for the larger values of v most, but not all, local maxima are immediately preceded by a positive event as defined above. This is illustrated in Fig. 2.4 where the events are defined by the line l. Thus (2.6,43) can also be interpreted as a good approximation to the number of peaks per unit time that are greater than v. It follows that the distribution of peaks per unit time is given approximately by
dv 27t вг
and has the form shown on Fig. 2.12.
|
Fig. 2.12 Distribution of peaks per unit time. |
PROBABILITY OF A POSITIVE EVENT DURING TIME tx
We now wish to find the probability that a positive event, as defined above, will occur in a given time t^. Let t1 be divided into a sequence of equal intervals At such that the following two conditions are met
(i) At < r(v)
(ii) The probability of an event during any particular interval At is independent of whether an event has occurred in any previous interval. (See below for discussion of this condition.)
Since N+(v) gives the average time density of events, then the probability of an event in At is (for At —> 0)
p(v, At) = AtN+(v) = — (2.6,46)
r(v)
and the probability that there will be no event in At is
q(v, At) = 1— p = 1 — — (2.6,47)
r(v)
Hence the probability that there is no event in n successive intervals is, by virtue of condition (ii) above,
*щШ) = (i-^j)"
If a positive event is identified with “failure” of a system, then clearly q(v, n At) is the probability of “survival”! for a’time tx = n At, i. e.
![]()
![]()
![]()
![]() (2.6,48)
(2.6,48)
Hence the probability of failure is
(2.6,49)
For large times (the usual practical case) n may be very large and the term in parentheses may be represented by its limit
![]() (2.6,50)
(2.6,50)
so that the survival probability is
(2.6,51a)
and the failure probability is
![]() p(v, tx) = 1 — e~h/r{v)
p(v, tx) = 1 — e~h/r{v)
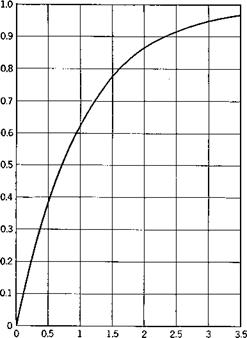
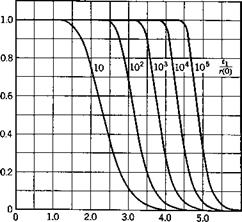
This result is general, and can be applied for any stationary random process. If the process is the Gaussian one previously discussed, then r(v) is given by (2.6,44), and (2.6,516) becomes
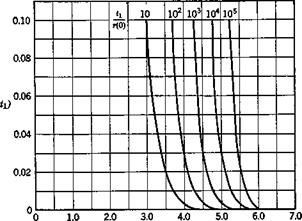
Equations (2.6,516) and (2.6,52) are plotted in Fig. 2.13. It should be noted that the probability of failure associated with t± = r is (1 — 1/e) or 0.63, and that the curves in (6) fall rather steeply over a fairly narrow range of v. Equation (2.6,51a) is a particular case of the Poisson distribution, for zero events in a time tv
f A more rigorous treatment of survival probability covering nonstationary and non-Gaussian processes is given by Rice and Beer (ref. 2.8) and is applied to launch vehicles by Beer and Lennox (ref. 2.9).
|
|
|
|
|
|
Fie. 2.13 Failure probability.