THE MECHANISM OF CIRCULATION IN FOIL SECTIONS
The lift produced by a finite-span airfoil, such as a plate for example, or an airplane wing, can physically be understood as the upward reaction to a downward deflection of a tube or cylinder of fluid having a diameter equal to the span of the lifting element. In a foil section (in two-dimensional flow) there is no permanent deflection. Therefore, lift or normal force produced, must rather be explained as the result of circulation.
|
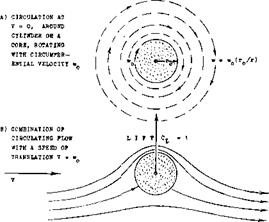
Figure 11. Theoretical flow pattern of circulation around circular cylinder or vortex core. At each and every point, the local velocity and direction corresponds to the geometrical sum of ;(V – p w). |
CIRCULAR CYLINDER. Circulation can best be understood by considering the circular cylinder as in figure 11. There are several methods of leading a certain portion of the air flow over the top, one of which is rotation, thus producing the so-called Magnus force to be discussed further in the chapter dealing with “blunt bodies". At this point, we will only make the statement that a “circulating" motion “around" the cylinder is set up by rotation. More fluid passes over the upper and less under the lower side; and the average velocity is increased and decreased, respectively. According to Bernoulli’s basic law, the static pressure along the surface of the body is thus reduced on the upper or suction side, and it is increased on the lower or pressure side. The result is a lifting force, id est a resultant of the pressure distribution the direction of which is normal (vertical or lateral, as it may be) to that of the basic stream of fluid and/or to the axis of the cylinder. The configuration as in the illustration thus yields a lift coefficient ^ i.4s while the theoretical limit for the flow pattern as in figure 11, would be 4тг ~ 12т.
LIFTING LINE. When reducing the diameter of the Magnus cylinder mentioned above, we finally arrive at a "rotating line.” Together with the surrounding circulating (but not rotating) field of flow, that line represents a vortex (11), and since it develops lift (if restrained to remain at, or if "bound" to its location) that vortex is a "lifting line." The flow pattern of this line, as that of any other vortex, is characterized by the circumferential velocity
w ~ 1/ r ; or: (w r) =. constant (2)
where r = radial distance of the fluid particle considered. As ‘r* increases, ‘w’ reduces (eventually approaching zero). On the other hand, when approaching the center of the vortex, the velocity ‘w’ theoretically approaches infinity. Actually, there is always a core within which viscosity (ll, b) slows down the circulating motion, reducing it to rotation (similar to that of a solid cylinder as in figure 11,a).
THE CIRCULATION of the lifting line considered is
Г = w 2 rir in (mVs) (3.)
where (2 гТГ) = circumference of the circle with the radius ‘r’ at which the velocity is ‘w’. When going around the lifting line, or around a rotating cylinder, or around a lifting foil by a 1000 different ways, we arrive at the
|
|
|
TWO-DIMENSIONAL ANGLE OF ATTACK 0<° o l—— 1—– 1—– 1—– 1—– 1—– 1———- /о Ю 2.0 Зо о Figure 12. Lifting characteristics of a round – edged, id est elliptical section. |
integral representing the same circulation as above:
Г — /w ds in (m2/s) (4)
where ‘s’— length of the way once around. This circulation represents the lift produced by any lifting device, or by any section of a wing, around which the integral is taken.
FOIL SECTIONS, as used in wings or anything similar in flatness such as a plate for example, are not lines; і in fact, only a mathematician can produce lift by means of a line. To understand the function of a wing section, we might say that at an angle of attack, the pressure side "leans" against the oncoming flow, thus forcing a certain volume of air to go around the usually rounded leading edge (nose), from the lower to the upper or suction side. Along the inclined and possibly cambered upper side, the stream of fluid is then lead down again. The airfoil is thus a device which forces certain stream tubes to go over the top. Theoretically this is not so certain, however. In an ideal, completely non-viscous fluid, the flow would pass around the trailing edge, from the lower to the upper side, and from the stagnation point near the leading edge, around the nose, to a corresponding rear stagnation point, at the upper side, near the trailing edge. The resultant lift would be zero, while there would be a "positive" pitching moment, tending to turn the foil to higher angles of attack.
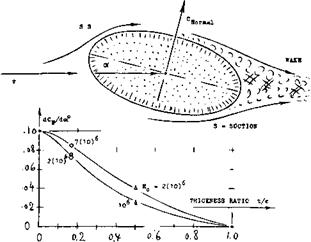
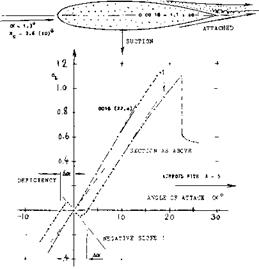
ELLIPTICAL SECTIONS. To illustrate this flow pattern, the lift of an elliptical section having a trailing edge as round as the leading edge, is presented in figure 12. Disregarding some secondary variations of the CL (ex) function, it can be said that the lift-curve slope is simply reduced in comparison to that of a conventional airfoil section. The flow is evidently separated from the round trailing end; and the two separation "points" move, together with the wake, steadily around the end from the pressure towards the suction side, as the angle of attack is increased. Consideration of the pitching moment gives some more insight into the flow pattern. At Rc= 2(10)fe , the center of lift is in the vicinity of 15% of the chord (strong suction forces along the upper side of the section nose, in combination with flow along the convex lower side, possibly to the very end of the section). The lift-curve slope as shown is the minimum. Since separation is a function of boundary layer conditions, the characteristics of the

section in ffgure 13 vary with Reynolds number. The lift-curve slope increases slightly as that number is increased. As the number is reduced below 10& , the slope increases also; and it reaches values very considerably above those of conventional foil sections, probably as a consequence of early laminar separation from the lower side, in combination with attached flow around nose and suction side (reattachment after laminar separation). This flow pattern is confirmed, at Rc between (3 arid
6) Ш5 , by Cp between 0.05 and 0.02 (which means Cq# up to 0.3), by a location of the lift force in the vicinity of 30% of the chord, arid by a maximum coefficient CLx approaching
1.0. – As shown in figure 13, the lift or normal force of elliptical sections reduces with their thickness ratio. Naturally, at t/c = 1, that :iis for a circular cylinder, lift (or lateral force) is zero. [23] [24] [25]
|
|
REVERSED 0012. After what is said about round and sharp edges, the lift of the 0012 section as in figure 14- should be expected to be very poor wheri reversing the direction of flow or flight. Surprisingly enough, the section tested has a lift-curve slope not only as high as in the conventional direction, but even slightly higher. There is first the leading-edge flow. As found in many tests with flat plates, a sharp leading edge is "no" obstacle for the flow to get around, and to continue (after a small local separation) along the suction side. To explain the increased lift-curve slope, we may suggest two possible reasons. One is that the round but separated trailing edge acts like a blunt edge (to be discussed later). The other reason may be found in the volume (displacement) of foil plus wake. Increased velocities might thus help to produce higher lift. Of course, the maximum lift coefficient of the section with the sharp edge leading, is but 0.8, in comparison to 1.3 in the conventional direction.-Testing conventional airfoil sections in reverse direction, is not as useless as it may seem at first. In the rotors of helicopters flying at higher speeds, it is quite possible that the inboard portions of the blades are moving against the air, with their sharp edges first.
LIFT COEFFICIENT. In applied arodynamics3, the term “circulation” is not used very much. The lift ‘L’ referred to the lifting area’S’, and to the dynamic pressure ‘q’ of the fluid flow, is represented by the non-dimensional coefficient
CL * L/qS * 2 Г/cV (5)
while the circulation producing the lift, is
/“=CL cV/2 in (mVs) (6)
As a function of the angle of attack ‘oc’, the lift of a flat and thin plate (in two-dimensional flow) corresponds theoretically to
C[_ = 2 IT sinoC (7)
At small angles, the lift-curve slope is
dCL/dcX = 2ir; dCL/da°= 21^/180*» 0.11 (8)
and the "lift angle" (15) is:
do(/dCL= 0.5/rr; or = 90/lT2= 9.1° (9)
This function means that an angle in the order of 9 is theoretically required, in two-dimensional flow, to produce a lift coefficient equal to unity, through the use of a plate or any thin airfoil shape.
|
Figure M. Lifting characteristics of 0012 section in reversed flow (12,d). |
|
|
|
0.81 * NOSE RADIUS r/o 0.24* |
|
Rn = 5(10)° |
|
41* |
|
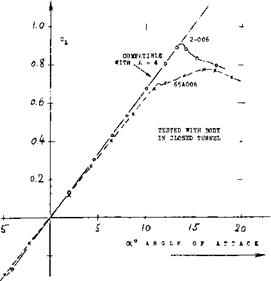
Figure 15. Lift of two 6% thick foil sections, differing in nose radius, tested in tapered wings with A = 4, on fuselage body (29). |
SHARP LEADING EDGES. We have mentioned (in connection with the reversed 0012 in figure 14*) that a sharp leading edge can very well produce a high lift curve slope. Theoretically, evaluated from (13,g), the loss of lift, when losing the leading-edge suction peak, is
acl= – (0.25/fr2) – Cl do)
This would be 2.5% at CL= 1, and it would be "nothing" at small lift coefficients. We have evaluated lift-curve slopes as a function of the leading edge radius ratio (r/c) for the 4-digit sections (31,c) as well as for a series of more or less sharp-nosed 6% sections (13,g). The conclusion is, that in a 6% section, about 5% is actually lost when making the leading edge perfectly sharp, as in a double wedge section, for example (having the same location of maximum thickness). This much is indicated in figure 21 as an increase of the lift angle at t/c —0. Sharp-nosed sections (with a certain trailing-edge angle) can also display a lift deficiency (non-linearity) near zero or symmetrical lift coefficient. The losses of momentum at the sharp l’edge evidently cause an accumulation near the trailing edge. For example, double-wedge or double-arc sections as in (13,a, c) not thicker than 6%, already show the non-linearity.
![]()
![]()
 |
THE NOSE^ADIUS of a foil section is a function of thickness ratio and thickness location. One can change the radius, however, according to equation f 1). As an example, lift and drag of a 6% section are shown in figure 15. There are evidently losses of moment um in the flow when getting around the leading edge of a thin airfoil. The difference in the lift-curve slope of the two shapes tested, is some 7%. The optimum size of the nose radius will also be a function of surface roughness and Reynolds number (see later), and of the Mach number (see the chapter on “compressibility*’). The maximum lift coefficient must also be considered when selecting a radius for the leading edge; see “maximum lift and stalling".
|
|
For “lift angle” (doc/dCjJ see the “wing” chapter. NACA airfoil sections, other than ‘6’ series:
a) See NACA Wartime Report L-345.
b) ‘16’ Series, TN 976, 1546, 2951; TR 763 & 2951.
W. M. Kutta (Bavaria, 1911); N. E. Joukovsky (Zhuko – vskij) “father of Russian aviation” (1847/1921).
Lift (and drag) of the 0070 section, tested by the author, in the two-dimensional water tunnel of Fieseler Aircraft Corporation, 1939.
Influence of the trailing-edge angle:
a) Williams, Cuff Sections, ARC RM 2457 (1951).
See chapter “characteristics of control devices”. DVL, Modified 0015 and (Ю18, see (34,c).
Hoerner, 0070 in Water Tunnel, not published (IS). Batson, 0015 Modified, ARC RM 2698 (1943). Beasley, Lift Reduction, AD-455,356; see (27,d).
The 63 and 64 series sections have almost exclusively been tested in closed two-dimensional tunnels. There results have been disregarded in this text to a large degree. The value of the (38) data is found in the comparison of the foil sections tested, with each other.
INFLUENCE OF THICKNESS. Thickness means displacement. As a consequence, average fluid-flow velocities along the sides of foil sections are generally increased over those past a thin plate; and their lift-curve slope is theorectically expected to increase with the thickness ratio. As an extreme, we may again consider the circular cylinder. Assuming that we would manage by means of boundary layer control around the rear side, to displace the stagnation points from zero (at the forward side) and from 180° (at the rear side) both down toward 90° (at the lowest point), without losing any momentum, its lift curve slope would be dCL/dcx— 4ir, rather than = 2тг, as in thin foil sections. In theory, therefore, the lift angle (15) reduces (as shown in figure 21) as a function of the thickness ratio.
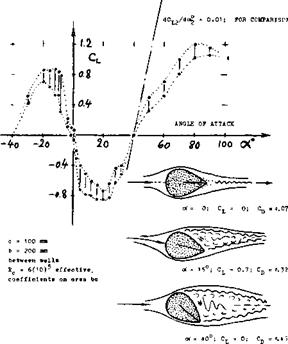
STRUT SECTION. "Streamline” sections, suitable to be applied in struts or in propeller blades near the hub, have usually higher thickness ratios than conventional foil sections. As an extreme example, the lift coefficient of an 0070 section (18) is presented in figure 16. The lift-curve slope at small angles of attack is strongly negative (!) up to ot^20°. The flow pattern proves that negative lift is the result of flow separation fr. om the upper side of the section. As a consequence of the well – attached flow along the negatively cambered lower side of the section, suction develops there, thus producing negative lift. As the angle of attack is increased, the lower side eventually produces predominantly positive pressures and a correspondingly positive lift. Also note that the maximum lift coefficient at oc=90°, fluctuating between 1.0 and 1.2, corresponds to suction forces developing a – round the section’s nose. – It is shown in (22,b) how the lift function of an airfoil with t/c = 68%, is almost perfectly linear, with a blunt trailing edge (see later). It can also be found in Chapter III of “Fluid-Dynamic Drag,” that the maximum lift of a section with t/c =40%, is increased from C^y ~0.8 to 1.15, when blunting the trailing edge to h – 0.4 t. Again, lift as a function of the angle of attack is practically linear. It may not be desirable, however, to have much lift or lateral force in a “strut.” The best method to keep such forces down, is to provide a well-rounded trailing edge.
TRAILING-EDGE ANGLE. The shape of all so-called streamline sections (designed for subsonic speeds) is such that the afterbody is more slender than the forebody. Flow separation is avoided or postponed in this manner. Figure 17 presents the lift coefficient of a foil section with thickness location at 40% of the chord. In combination with a thickness ratio of 18%, a trailing-edge angle (included by upper and lower side) of approximately 30° is thus obtained. As a consequence, when rotating the foil out of zero angle of attack, the boundary layer (id est its thickness, but not the material itself) switches from one side to the other. The growth at (and possibly some separation from) the upper side, and the suction of the attaching flow at the negatively cambered lower side, are so strong, that a negative lift-curve slope is produced at angles between plus and minus 1.5°. The positive lift – curve slope (above oc ^ 1.5°) is almost equal to that of the same type of section with the thickness located at 3C?*bf the chord. The later figure 33 includes a different example of trailing “wedge" angle on a comparatively small beveled portion of the chord. While any of the “wild" effect as in figure 17, is not evident, the lift-curve slope near zero lift, is noticeably reduced. Such an effect of the “wedge" angle is particularly known in control surfaces where effectiveness and hinge moment are both a direct function of that angle (as explained in the chapter on “control surfaces"). In figure 18. it is shown how the lift-curve slope (of symmetrical sections, around cx = 0) reduces, and the “switching" angle (defined in figure 17) increases, as a
|
HEAVY BOUNDARY LAYER
Figure 17. Lift as a function of angle of attack of a section having a large trailing-edge angle. |
function of the trailing wedge angle (or of the half angles). At tans between 0.3 and 0.4 (that is between 16 and 22°) the slope of the lift seems suddenly to switch from positive to negative. Here again, the Reynolds number (affecting boundary-layer conditions) must be expected to have an influence. As seen in (20,a) for example, “switching" and negative lift-curve slope are not obtained at smaller R’numbers (below 106 ). Since delay and switching do not take place in round-ended (elliptical) sections, it can be concluded that a sharp trailing edge (with a certain wedge angle) is necessary for producing the flow pattern described.
|
Figure 18. Lift-curve slope and “switching” angle of thick foil sections as a function of the trailing-edge angle as defined in the graph. |
BLUNT TRAILING EDGES have an effect upon section characteristics which is precisely opposite to that of large trailing wedge angles. In fact, the angle included by upper and lower side is naturally reduced when thickening the trailing edge. Figure 19 presents an example where an 0018 airfoil was shortened by cutting off 5% of the chord from the trailing edge. Results of blunt edges similar to this one are generally as follows:
(a) Any weakness of the lift-curve slope in the range of small angles of attack (if any) can be cured by making the trailing edge thick and blunt. This may again be important for control surfaces such as ailerons.
(b) 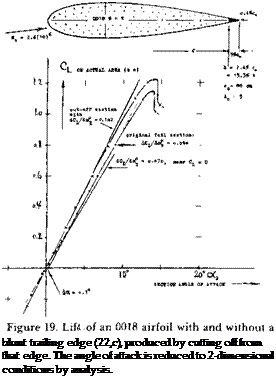 The lift curve slope is somewhat increased above that of the same section having a conventional sharp trailing edge. In the case of figure 19, the slope (reduced to two-dimensional condition) is a full 10% increased over that of the original section. If considering lift (id est, L/q of the wing as tested) rather than the coefficient (referred to span times chord shortened from the trailing edge), we still obtain 5% more lift for the section with the blunt edge than for the sharp-edged original section.
The lift curve slope is somewhat increased above that of the same section having a conventional sharp trailing edge. In the case of figure 19, the slope (reduced to two-dimensional condition) is a full 10% increased over that of the original section. If considering lift (id est, L/q of the wing as tested) rather than the coefficient (referred to span times chord shortened from the trailing edge), we still obtain 5% more lift for the section with the blunt edge than for the sharp-edged original section.
(c) The maximum lift coefficient of the section in figure 19 is noticeably increased. However, if considering CLx-/C^m;n as a figure of merit for a wing, the test does not show any advantage of the blunt-edged (102) over the original section (142). It is only when thickening (rather than cutting off from) the trailing edge, thus keeping the ratio t/c = constant, that a very small improvement of the figure of merit (143), can be found (23,c)for the type of section as in the illustration, for a very modest thickness ratio of the trailing edge (in order of h/c = 0.5%, or h/t = 3%). Full-scale, this might be 1 cm; but the edge should be sharp to be of benefit.
 Results of another foil section are shown in figure 20. When cutting off a small piece of the trailing edge, the boundary layer accumulation as indicated in the illustration is evidently cut down too, so that the slope of the lift coefficient (referred to the reduced area) increases, to a certain maximum as shown. For similar results on 0012 see (22,a).
Results of another foil section are shown in figure 20. When cutting off a small piece of the trailing edge, the boundary layer accumulation as indicated in the illustration is evidently cut down too, so that the slope of the lift coefficient (referred to the reduced area) increases, to a certain maximum as shown. For similar results on 0012 see (22,a).
INFLUENCE OF FRICTION. In reality, the lift angle is never as low as predicted by theory (equation 9 ), not even in sections with “optimum” thickness and shape. Because of skin friction and boundary layer growth along the suction side of lifting foil sections, the angle necessary to produce a certain lift coefficient is larger than according to circulation theory. The growth (displacement) of the B’layer is usually of such a nature, however, than the straightness of the Cl (o0 function is preserved for practical purposes, for all but the higher thickness ratios, within the range of
t NACA, 0025/35 IN FST (32,c) П ARC, ООІ5/ЗО, 3(ЮГ (36,a) A FROM VARIOUS OTHER SOURCES <C> AVA, AT 4(ЮГ & З(ЛО)[26] (6)
0 ![]()
 NACA, IN VDT, 3(10)®. (31,с) V ARC STRUTS AT 3(10Г (36,о) x DVL (HOERNER), CLARK-Y (34) – NACA 63/64 IN 2 DIMENS (38)
NACA, IN VDT, 3(10)®. (31,с) V ARC STRUTS AT 3(10Г (36,о) x DVL (HOERNER), CLARK-Y (34) – NACA 63/64 IN 2 DIMENS (38)
1 AVA, J0UK0VSKY SERIES (4,b)
![]()
![]()
![]()
![]()
![]()
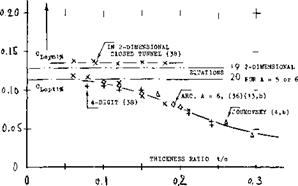
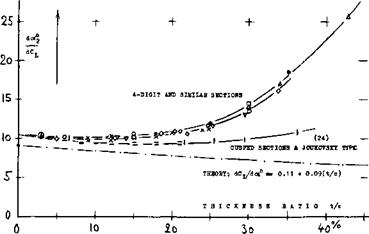
lift coefficients excepting those approaching the maximum. Sectional lift angles are plotted in figure 21, as a function of the thickness ratio. It is seen that the theoretical prediction mentioned above, whereby the lift-curve slope should increase with the thickness ratio (so that the lift angle would reduce), does only come true, say up to t/c = 10%. The boundary- layer growth and the theoretical influence of thickness evidently cancel each other to a large degree, so that the lift angle in the range of t/c between 0 and 12 or 15%, comes out as a more or less constant value in the order of
(dcx°/dCL)2 = 10° (U)
Where the subscript ‘2’ indicates conditions in two-dimensional flow (id est at A =00).
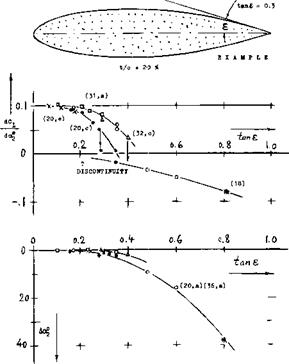
SECTION SHAPE. Although there seems to be an influence of testing technique (l4), conclusions as to the influence of section shape upon the lift angle in figure 21, areas follows:
(a) Sections with cusped (concave) afterbody contour (such as the 63 and 64 series, in particular) have the highest lift-curve slopes (21) and they maintain a lift angle slightly below 10°, possibly up to t/c = 30% (20,e).
(b) All "conventional" sections (such as the 4-digit series ) with convex afterbody contour and trailing-wedge angles of corresponding magnitude, display a reduction of their lift – curve slope) above t/c = 10 or 12%.
(c) Roughness, even if only applied in form of a stimulation strip near the leading edge, increases the lift angle of sections, particularly within the range of higher thickness ratios.
"EFFICIENCY." The loss of lift of afoil section as against potential theory, can be interpreted as an effective reduction of the wing chord ‘c’ =a c. Consequently, in two-dimensional flow, in comparison to thin-plate theory (equation 2o):
C^- 2 air sincXg ; dCL/do(^= 2 атг ; do<2/dCL= 0.5/air (12)
The commonly used airfoil sections have efficiency factors (30) in the order of a = 0.9. At higher thickness ratios as in figure 21, (dc*/dCj_) increases considerably. Formation of a heavy boundary layer at (and eventually flow separation from) the suction side, displace the outer flow, away from the trailing edge so that the circulation becomes progressively reduced. Theory has tried analysis of this effect; in fact, one author (27) has gone so far as to predict the circulation of a certain foil section from a boundary-layer survey taken at the trailing edge.
10-
IS– (7,a)(2B, h)
Damir
|
lo* —y— |
![]()
![]()

![]()
![]()
![]()
![]() ROUGHNESS. The section-drag coefficient increases with the thickness ratio. Skin friction can also be increased, above that as for smooth surface condition, by roughness. Figure 22 presents doC/dC^ of various "conventional" foil sections having thickness ratios between 12 and 17%, as a function of their minimum section drag coefficient (as tested at small lift coefficients). The lift angle increases considerably; a value twice as high as that for smooth condition, is not impossible, provided that skin friction is sufficiently increased by surface roughness and/or other "obstacles," For practical purposes, the slope of the lift angle in figure 22 might be approximated by
ROUGHNESS. The section-drag coefficient increases with the thickness ratio. Skin friction can also be increased, above that as for smooth surface condition, by roughness. Figure 22 presents doC/dC^ of various "conventional" foil sections having thickness ratios between 12 and 17%, as a function of their minimum section drag coefficient (as tested at small lift coefficients). The lift angle increases considerably; a value twice as high as that for smooth condition, is not impossible, provided that skin friction is sufficiently increased by surface roughness and/or other "obstacles," For practical purposes, the slope of the lift angle in figure 22 might be approximated by
A(do<7dCL) = 180 CDimln (13)
(26) * Influence of skin friction on lift, experimental:
a) Betz, Lift/Drag, ZFM 1932 p 277; NACA TM 681.
c) See results function of Reynolds number (40).
d) Batson, B’layer at Tr’edge, ARC RM 2008, 1998
(27) Analysis of lift as a function of drag:
a) Weinig, Lift Deficiency, Lufo 1938 p 383.
b) Sniper, Lift f(Drag), ZFM 1933 p 439.
c) Preston, Boundary Layer, ARC RM 2725 (1953).
d) Beasley, Lift Reduction Due BL, ARC RM 3442
(28) Influence of surface roughness on lift:
a) Wieselsberger, Ringbuch IA9 (Durand IV p 19).
b) See Ergebnisse AVA Gottingen III (1926) p 112.
c) Jones, 0012 &: RAF-34 roughness, ARC RM 1708.
d) Hoemer, 0012 in Wat’Tunnel, unpublished (1939).
e) Hooker, Surface Roughness, NACA TN 457 (1933).
f) Muttray, On Joukowsky Sections, NACA TM 768.
g) Bradfield, With Metal Gauze, ARC RM 1032 (1926).
h) Wood, Corrugated Surface, NACA T Rpt 336 (1929).
(29) Maki, 64A010 Modifications, NACA TN 3871 (1956).
(30) Neely, 44(12 to 24) A – 8 to 12, NACA TN 1270.
(31) Airfoils with A = 6 in NACA V’Density Tunnel:
a) Jacobs, 78 Related Sections, T Rpt 460 (1933).
b) Jacobs, Function of R’number T Rpt 586 (1937).
c) Jacobs, Various Corrections, T Rpt 669 (1939); this report is the best of the series.
e) Pinkerton, Various Sections, T Rpt 628 (1938).
f) Jacobs, 23012 Type, see references (33,b, c).
(32) Airfoils with A = 6, in NACA Full-Scale Tunnel:
a) Silverstein, Clark-Y Airfoil, T Rpt 502 (1934); section named after Colonel V E Clark (1886 to 1948).
b) Goett; 0009, 0012, 0018 Airfoils, TR 647 (1939)
c) Bullivant, 0025 Sc 0035 Foils, TR 708 (1941).
(33) Investigations and results on 23012 airfoils:
a) Jacobs, FS and V’Dens Tunnels, TR 530 (1935).
b) Jacobs, in V’Density Tunnel, NACA T Rpt 537.
c) Jacobs, Foil Series in VDT, NACA Rpt 610 (1937).
d) NACA, with Flaps, T’Rpts 534 (1935), 664 (1939).
e) ARC, in CAT’, RM 1898 (1937); RM 2151 (1945).
f) Doetsch, In DVL Tunnel, Ybk D Lufo 1939 p 1-88.
(34) Airfoils as tested in the “large” DVL wind tunnel:
a) Doetsch and Kramer, Lufo 1937 p 367 and 480; also Ybk D Lufo 1937 p 1-69, 1939 p Ї-88, 1940 p [-182.
b) Hoerner, Clark-Y Series, DVL Rpt Jf 208/3 (1940); also in small tunnel, ZWB FB 65 (1934).
c) Collection ol DVL Results, ZWB FB 1621 (194.3).
d) For DVL (and other) results see also ref (6).
e) Pressure Distributions. Ringb Luftf Tech LA,11.
— 6
DISCONTINUOUS DH0P DUE TO LAMINAE SEPARATION (SCHMITZ)
NACA CLARK-Y FST (32,a) ARC (32,a) ft RAF (36,e) AVA WITH t/o = 12* (6) NACA 12 * SECTIONS (6)
І0 [27] [28]
2 – 14
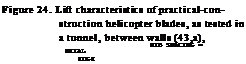 |
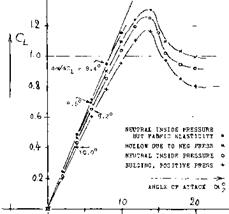
PRACTICAL CONSTRUCTION (44). The boundary layer developing along the chord of foil sections, can be disturbed (made heavier) by skin irregularities (pro – turberances) due to fabrication. A different effect is deformation of section shape. Portions of helicopter blades were tunnel-tested (44,a). These blades consist of a solid nose section and a fabric-covered afterbody supported by ribs (with spacings equal to 1/3 of the chord). As a consequence of pressure distribution (due to lift) the fabric deforms itself. Because of porosity (leakage) there may also be a negative pressure inside. In helicopter blades, positive pressures may also develop inside, caused by centripetal acceleration. The experimental results as in figure 24 show:
(a) When the fabric is bulging, the lift-curve slope is reduced, probably because of trailing-edge angle and increased drag.
(b) For a negative inside pressure of 100 lb/ft (at an estimated dynamic pressure of the same but positive order) the sides of the foil section are somewhat hollow. As a consequence of reduced trailing-wedge angle, the lift-curve slope is as high as that of a smooth and solid 0012 section.
(c) In samples where the fabric tension is not very high, a deformation takes place in such a manner that the pressure side becomes somewhat hollow, and the suction side bulging. The resultant section camber, increasing with the lift coefficient, produces a particularly high lift curve slope, in the order of 0.12 as tested in a closed-type tunnel between walls (21).
(d) The maximum lift coefficient varies corresponding to the lift-curve slope.
|
|
|
14 |
|
+ |
|
/7 2(10) |
In subsonic aerodynamics nearly all wing sections designed for the production of lift have a cambered mean line. The shape of the mean line selected influences the chordwise lift distribution, the zero lift angle, the lift at an angle of attack of zero, the lift at the maximum lift drag ratio and the maximum lift coefficient. The type of mean line used depends on the airfoil series type, and its application.
CAMBER LINES. Mean lines used in the most widely known families of wing sections, are shown in figure 8. These lines are characterized primarily by the location of their tops (in % of foild chord) and by their camber ratio f/c (see figure 1). Although circular arcs are not really used in conventional foil sections, their geometry lends itself to analysis. In particular, the angle at the edges, as in the sketch (figure 27) of such a mean line is
tany" – 2 f/x
where x = distance between f and trailing or leading edge.
ZERO-LIFT ANGLE. In two-dimensional flow, the “symmetricar lift coefficient (see equation 210 for a circular-ar mean line (with x = c/2) is obtained at zero angle of attack. In terms of the angle at the trailing edge, the perturbation or circulation velocity at that edge is
w = Vy; Г— w 2 (с/2)тг = ТГc Vy* in (m2/s) (16) so that the lift coefficient due to camber (at c* — 0) is: — Г/ (с V) = 7ry = 4irf/c (17)
The angle of attack necessary to reduce the C(_ due to camber to zero, corresponds to do^/dC^ — 0.5/77-. Therefore, in a section with circular-arc camber, this angle is theoretically
cxo= -2 f/c = —(360/tt ) f/c = — 1.15(f/c)%
degrees(18)
Zero-lift angles are plotted m figure 25, as a function of camber location. Since the angle is related to the tangent to the camber line at the trailing edge, foil sections of the 230 type, having a straight camber line over most of their afterbody, show less negative zero angles than the more evenly cambered 4-digit sections. Foil shapes with thickness ratios exceeding 12%, have zero angles somewhat smaller (less negative) than those shown in the graph, for t/c between 6 and 12%. The angle of zero lift also increases (to somewhat more negative values) as the camber ratio is increased above a few percent.
0 o. l 0-2 o. l ah ».s o. C, o. l
Figure* 25. Alible of attack for /его lift, for camber ratios up to 2 or 3%, as a function of the location of camber along the section chord.
Design CLt, The maximum camber, f, of NACA 1 and 6 series airfoils is generally given in terms of the design CLi, and can be found from the equation
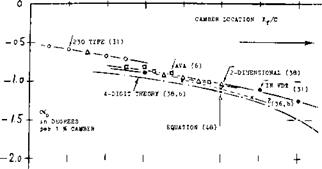
PRESSURE DISTRIBUTIONS are shown in figure 26, for one and the same lift coefficient, one around a straight, and the other for a cambered foil section. The sharp suction peak found at and above the leading edge of the symmetrical section, is avoided bv cambering the edge into the oncoming flow. Doing this (between 1910 and 1920, or so) simple imagination was applied, with the idea of helping the flow to get around the edge (from the lower to the upper side). Meanwhile, it has been discovered that under certain conditions, suction peaks do as follows:
they prevent laminar separation, making the B’laver turbulent; they do not necessarily cause cavitation in hydrofoils; they may even be desirable at higher subsonic speeds.
Nevertheless, some small amount of camber, say f/c = (1 or 2)% can successfully be used in the design of wings.
|
|
|

![]()
![]()
![]()
![]()
cC — -6.34 Сц
Airfoils tested in DVL High-Speed Tunnel:
a) Gothert, In High-Speed Tunnel, ZWB FB 1490-
b) Gothert, Symmetrical Sections, ZWB FB 1505/06.
c) Gothert, Cambered Sections, ZWB FB 1910 (6 Vol).
Airfoil sections reported by British ARC:
a) Jones, 0015 and 0030 in CAT, RM 2584 (1952).
b) Hilton, 18 Sections High Speed, RM 2058 (1942).
c) Williams, Strut Sections, RM 2457 (1951).
d) See also references (5) (6) (7,c) (28,c) (40,b).
e) ARC, Investigations in the Compressed Air Tunnel, RM 1627 (Rnumber), 1635 (RAF-34), 1717 (RAF – 69-89), 1771 (airscrew sections), 1772 (RAF-34), 1870 (Joukowsky), 1898 (23012), 2151 (23012 wing), 2301 (circular-arc backs), 2584 (0015 — 0030).
f) Pankhurst, Aerofoil Catalogue, ARC RM 3311 (1963).
Modifications of the NACA 4-digit series:
a) A modification as to thickness location is presented by Stack, “Tests at High Speed”,
NACA TR 492 (1934); also found in TR 610.
b) Elimination of cusped contour, . . . Loftin, “A”
Series, NACA TR 903 (1948); also TN 1591 к 1945.
Foil sections tested in two dimensions by NACA:
a) Doenhoff, Low-Turbulence Press Tunnel, TR 1283.
b) Abbott к von Doenhoff, Collection, TR 824 (1945); also “Wing-Section Theory”, McGraw Hill 1949.
c) Loftin, At Very High R’Numbers, TN 1945 (1949)
8cRpt 964 (1950); also RM L8L09 with 34 sections.
d) See also reports in reference (37,b).
e) Loftin, Modified 64-010 Section, TN 3244 (1954).
f) McCullough, 0006/7/8 in Tunnel, TN 3524 (1955).
g) 64-X10 Sections, TN 2753,2824,1945,3871; R 824.903.
SYMMETRICAL FLOW. Pursuing the original idea of camber, it is possible to “optimize” the shape for a certain lift coefficient by giving the section such a camber that the flow passes smoothly along both sides of the leading edge, without going around that edge. We will call this condition “symmetrical”, that is in regard to the local flow past the leading point of the camber line. For circular-arc camber (at 50% of the chord) the sym-
![]()
metrical lift coefficient is expected to be as in equation (17) so that
CL = 4Tff/c = 0.126 (f/c)% (19)
For camber positions between 30 and 40% of the chord, camber required to make the leading-edge flow symmetrical, must be expected to be slightly smaller than corresponding to this equation. However, in wings with finite span, stream curvature reduces the effective camber by
A(f/c) = — (0.25/tt) Cj/ A (20)
For practical purposes (with A in the order of 6) the “symmetricar lift coefficient for commonly used foil sections, is therefore ; approximately
cL<ym= 0.115 (f/c)% (21)
This function is confirmed in figure 27, by results obtained from pressure-distribution tests. Selecting the center of the “bucket” formed by their drag coefficient, “symmetrical” lift coefficients can also be obtained for laminar-type foil sections (21).
|
Figure 27. Symmetrical and optimum lift coefficients as a function of camber, for airfoil sections with t/c between 6 and 12%. |
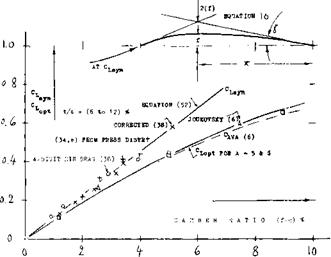
OPTIMUM LIFT coefficients are meant to indicate a minimum of the section-drag coefficient. In “ordinary” foil sections such minimum is not very well defined. Figure 27 leaves no doubt, however, that the optimum are lower than the symmetrical coefficients. As camber is increased, ^ more and more deviates from and below the straight line as for symmetrical flow (equation 52). A sufficient amount of camber is thus found to reduce the viscous or sectional component of drag, that is at and around a certain lift coefficient (such as Cl =■ 0.3 or 0.4, at which an airplane may cruise from New York to Europe).
|
Figure 28. Symmetrical and optimum lift coefficients per percent of camber (for camber ratios up to 2 or 3%) as a function of thickness ratio. |
THICKNESS RA TIO. Figure 28 shows the value of the optimum lift coefficient per 1% camber, as a function of the thickness ratio. It is seen that as deter
mined on the basis of section-drag readings, reduces considerably at higher thickness ratios. This result can be explained by the fact that in cambered sections, the weakest part of the boundary layer is near the trailing edge (where the layer is heavy and the pressure gradient positive, thus favoring separation). As a consequence, minimum section drag (and possibly a symmetrical flow pattern) is obtained at lift coefficients smaller than theoretically expected.
“LAMINAR”FOIL SECTIONS are discussed in Chapter VI of “Fluid-Dynamic Drag”. Among the shapes under
(d) in section (A), the ‘64’ series (with maximum thickness at 38% of the chord) represents a tentatively effective, yet conservative type of laminar-flow sections. To really obtain the benefit of a section drag coefficient as low as 0.004 (which is half of that of a 4-digit section) certain requirements have to be observed, (a) A minimum thickness (say t/c = 10%) is needed to maintain a favorable pressure gradient, (b) The surface has to be kept as smooth as possible, (c) The low-drag “bucket” should be around the cruising lift coefficient. — When giving a ‘64’ section the optimum or the symmetrical camber, the “bucket” moves from zero lift to the design lift coefficient, without losing any or much of its size. For example, the 64-210 section (38,b) is found to have a low drag coefficient at between 0.1 and
0. 3. The ACl – 0.2 is almost doubled (that is, to 0.4) when using t/c = 12%, even at a design lift coefficient Cl*l = 0.4, as in 64-412.
 4. LOW REYNOLDS NUMBER
4. LOW REYNOLDS NUMBER
The operating Reynolds number is very low for model aircraft wings, birds, bugs and other devices such as wings and propellers used on high altitude remote piloted vehicles. Typical values have been listed (41 ,c) as
R = 7,000
R = 20,000 R= 200,000 R = 200,000
R = 60,000 to 200,000
|
|
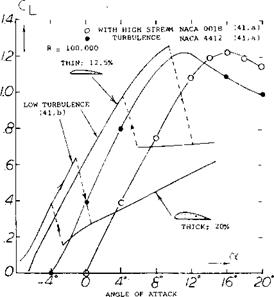
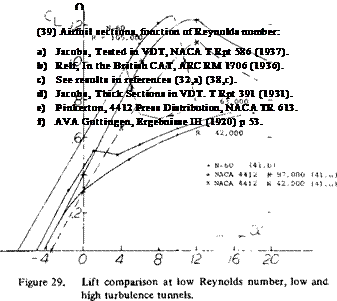
Turbulence Effects. Airfoil test data at low Reynolds number is limited to that obtained by early investigators and for use in conjunction with model airplanes. The systematic airfoil investigations run in the highly turbulent VDT (41,a) are considered to be questionable because of the effect of turbulence on the boundary layer. Compared to the data of (41,a) the low Reynolds number data of (41,b) run in a low turbulence tunnel show at R < 100,000 higher levels of drag, lower values of Cimax m^ а lift hysteresis after stall, as illustrated on
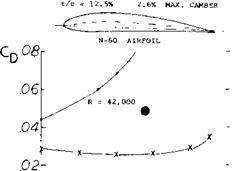
figure 29. The reduction of drag obtained at R < 1.05 was anticipated by the work of (41,b).
 |
 |
Thickness Ratio and Camber. For the best performance at low Reynolds numbers the thickness ratio should be low and camber high, whereas at R r 1.0 s the higher thickness distribution of a Clark Y or similar airfoil gives better performance, figure 30. This may explain the type of wing section found in nature and the shape preferred by the early investigators. Airfoils with high thickness ratios have much lower values of CLy as shown on figure 31. Here, increasing the thickness ratio from 12 to 20% reduced CLX by one-half. The test in the VDT indicated that large gains can be made by making the flow turbulent. A wire in front of the airfoil can be expected to give the desired flow at low Reynolds numbers.
|
Figure 31. Lift at R – 100,000 for high and low turbulence at t/c – 12 to 20%. |