Turbulence noise at low Mach numbers

5.1 Isothermal free jet

Considering the sound production of a turbulent free jet. This is the flow with a velocity U0 at the outlet of a pipe of diameter D. Turbulence is an unsteady chaotic fluid motion which appears when viscous forces are small compared to non-linear convective forces. This corresponds to high Reynolds numbers ReD = UqD/v. We limit ourselves to a low Mach num­ber flow M = Uq/oq ^ 1 of an air jet surrounded by air with the same temperature as its surroundings. The prediction of the scaling rule between the power of this sound source and the Mach number was a major suc­cess of the theory of Lighthill (1952-54). As stressed by Powell (1990), the scaling law was predicted before it was corroborated by experiments. The steps taken by Lighthill were, however, quite intuitive and justification of some of these steps came only long after the original publication [Mor – fey (1973),(1976),(1978), Obermeier (1975)]. We now follow the Lighthill prodecure [1954].

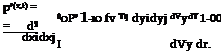Firstly Lighthill assumes that there are no external forces working on the flow and that the effect of walls can be neglected. In free field conditions equation (99) simplifies to:

This implies that the solution we are seeking for is, at most, a quadrupole field. In fact, we have imposed this by assuming that there are no external forces acting on the fluid and the potential monopole sources were neglected. Please note that in the analogy of Lighthill, p is used as aeroacoustical vari­able. In the next section we will discuss why this choice can be important. Carrying the time integration and using the far field approximation we find:

The sound appears to be produced mainly by large coherent vortex struc­tures with a length scale of the order of the pipe diameter D. For such scales the Reynolds number is large. We therefore expect the Reynolds stress ten­sor pvivj to be much larger than the viscous stress tensor Tij [Morfey (1976)]. Furthermore, at low Mach numbers variations in temperature and density are negligible [Morfey (1973), Morfey et al. (1978)], which implies that we

Figure 7. Overall acoustic sound power level (OAPWL) of the sound radiation from an isothermal free jet as a function of the jet Mach number: comparison of theory with experimental results [Fisher et al. (1973),Viswanathan (2009)].

can use the approximation proposed by Lighthill (1952-54):

Tij & poViVj. (127)

For a circular jet cross section the dominant frequency corresponds to a Strouhal number of unity. Hence the dominating frequency is U0/D and the corresponding acoustic wavelength is D/M = Dc0/U0. The sound source has a volume V of the order of D3. At low Mach numbers the sound source is small compared to the wave length. This implies that we can neglect

Substitution in (126) yields:

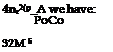
In terms of sound source power < P >

<P>

1 p U3 nD2

2 p0U0 4

where we assumed an isotropic radiation pattern. This famous global scaling rule of Lighthill (1952-54) appears to be valid up to Mach numbers of order unity. At these high Mach numbers the radiation pattern has a high forward directivity due to the Doppler effect and, due to refraction of sound by the shear layers, it displays a cone of silence around the axis. The fact that the theory remains valid up to relatively high Mach numbers can be partially explained by the fact that the convection velocity Uc of the vortices in the jet is only a fraction of the main flow velocity [Crighton et al. (1992)]. Typ­ically we have Uc/U0 « 0.3. Recent discussions on jet noise are Morris and Farassat (2002) and Viswanathan (2009) as well as the discussion in Part 2.

Obviously, by increasing the Mach number, the scaling law of Lighthill fails simply because the radiated power would become larger than the avail­able jet power 1 pU0 ^4Р-. Also the sound production mechanism changes drastically. The sound radiation from supersonic jets above M = 3 is largely due to hydrodynamic shear waves which display highly directional radiation patterns. Entropy effects due to temperature differences in the flow also be­come very important. In a supersonic flow the temperature typically varies from the stagnation temperature Tt to the isentropic expansion temperature T = Tt/(1 + (y — 1)M2/2). Starting from room temperature Tt « 300^ in the reservoir, M = 3 implies a main flow temperature T « 100^. Obvi­ously, such a flow is not isothermal and we can use many different definitions of the temperature or Mach numbers to characterize the flow [Viswanathan (2009)].

Finally, most supersonic jet are either over – or underexpanded, and there­fore display standing shock structures, which interact with vortices (turbu­lence) that give strong sound radiation. In some cases, this leads to spec­tacular self-sustained oscillation (jet screetch).

Note that approximation (128) is based on the fact that in a circular jet the characteristic Strouhal number for the sound production is of or­der unity SrD = Df/U = 0(1). In a planar jet of thickness H we find

SrH = Hf/U = 0(10 1), which again stresses that the assumptions are not trivial [Bjprnp et al. (1984)].

Turbulence noise is essential because, when all other sound sources have been suppressed, this will always remain as the minimum remaining noise production which we can achieve. Lighthill’s scaling law indicates that the most efficient way to reduce this noise is to reduce the flow velocity. The result derived for free-field conditions remains valid for confined flow. In the absence of resonances, one finds at low frequencies in a pipe p’ ~ poU0/co and < P >~ M6.

It is important to stress again that the analogy of Lighthill does not impose the quadrupole character of the source. Because we neglected the monopoles (no heat sources and negligible variation in density) and the dipoles (no external force acting on the “free” jet), the source has at most, a quadrupole character. Based on the integral formulation (126) the proce­dure imposes this assumed quadrupole character on the solution. So even if the applied model predicting the stress tensor Tij does involve density fluctuations and external forces, the formulation ensures that these contri­butions are ignored. This explains the success of such analogies [Schram and Hirschberg (2003)]. They filter out spurious sound sources due to errors in the estimation of the stress tensor Tij.