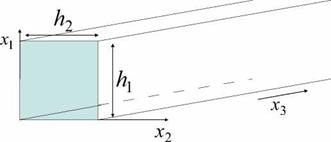
Waves in pipes
5.2 Pipes modes
We are considering propagation of harmonic waves p’ = pexp(iwt) in a duct with a uniform rectangular cross section, with the duct axis is in the x3 direction. The duct is delimited by rigid walls in the planes: xi = 0,xi = h1,x2 = 0,x2 = h2 (Figure 9). For such harmonic waves the wave equation
|
|
Figure 9. Duct with rectangular cross section.
(47) can be written as:
This is the Helmholtz equation.
Seeking a solution by using the method of separation of variables:
p = F(xi)G(x2)H(x3) . (139)
and substituting (139) in (138) we get:
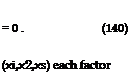 2 1 d2F 1 d2G 1 d2H
2 1 d2F 1 d2G 1 d2H
0 + F dxf + G dx2 + H dx3
|
1 d2F F dxl |
|
1 d2G G dx2 |
|
1 d2H H dxl |
|
[k2 – a2 – в2] |
As this equation should be valid for any value of x – in (140) should be constant:
|
Fm cos(amxi) , am, ; m 0? 1? 2? 3? … (146) |
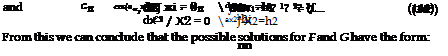
The constants a and в are determined by the boundary conditions of zero normal velocity at the rigid walls. The normal component of the pressure gradient, which is proportional to this normal velocity, vanishes at the walls:
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
![]()
The solution we are looking for is a linear superposition of these modes:
where the amplitudes of the modes are determined by the boundary conditions at the boundaries of the duct in the x3 direction. For each mode there is a cut off frequency (wmn)c below which the mode is evanescent. For example for the mode pi0 we have:
(wio)c = ПС0 . (153)
hi
The duct width should be larger than half the wave length to allow propagation of this first higher-order mode. The mode p00 is the plane wave mode and will always propagate.
Evanescent waves do not propagate energy. They decay exponentionally with the distance along the duct. In the low frequency limit ш ^ (umn)c the pressure perturbation due to an evanescent mode will decay faster than exp ^—mf-x^j. For mode (1,0) a distance hi is sufficient for a decay by a factor exp(n) « 23. All other higher-order modes will decay even faster.
Hence, the acoustic field will be dominated by plane waves in the low frequency limit for distances larger than the duct width away from discontinuities. This result will be applied in the following sections.
In this discussion we have neglected damping. In ducts damping due to visco-thermal losses at the walls is usually dominant. These effects on acoustical wave propagation are discussed in Pierce (1990), Bruneau (2006) and Rienstra and Hirschberg (1999). Damping, in presence of flow, has been extensively studied by Ronneberger and Ahrens (1977), Peters et al. (1993), Howe (1998) and Allam and Abom (2005).
5.3 Reflection at pipe discontinuities at low frequencies
We are looking at the reflection and transmission of plane acoustic waves at an abrupt transition at x = 0 between a pipe with uniform cross-section Si(x < 0) and another with uniform cross-section S2(x > 0) (Figure 10). Assuming that small perturbations of a stagnant fluid, as described by the
Figure 10. Reflection and transmission of waves at a pipe discontinuity.
linearized mass and momentum equations (44 and 45), the integral formu-
lation of the mass equation can be applied:
|
|||||
|
|
|
|||
to a volume V enclosed by the fixed surface S with outer unit normal vector П. The surface S is chosen to enclose the pipe discontinuity and cut the pipes at a distance of the order of the pipe diameter from the discontinuity. As explained in the previous section, the acoustic field in the pipes is dominated at low frequences by the plane travelling waves. This implies that the acoustic field is given by:
Pi = P+ exp(-ikox) + p – exp(ikox) (155)
where the index i = 1 corresponds to the x < 0 and i = 2 to x > 0. Using equation (53) we have:
S1(P+ – P-) – S2 (P+ – P-) ~ (C^S^ (P+ + P – ^ (156)
At low frequency the volume flux across the pipe discontinuity is constant and the flow is locally incompressible.
Assuming, f = 0 and integrating the momentum equation (45) along the x-axis, we get the linearized Bernoulli equation:
d Ґ2 , ,
Podt J v’xdx = p (xi) – p (x2) . (157)
In terms of plane waves we have:
p+ + p – – (p+ + p-) – (P+ -P-^ (158)
which implies that, at low frequencies cV/(c0S1) << 1, the pressure is continuous across the pipe discontinuity.
Thus, we have:
S1(p+ – p-)= S2(p+ – p-) (159)
and
p+ + p – = p+ + p – . (160)
In the form of a scattering matrix we get:
|
p- |
1 |
Co 1 Co to |
2S2 ] |
p+ |
|
. p+ . |
Si + S2 |
2S1 |
S2 – S1 |
_ p – . |
For an anechoic (non-reflecting) pipe termination of segment 2 (p— = 0) we have a reflection coefficient R = p—/p+ = (Si — S2)/(S1 + S2) and a transmission coefficient T = p+ /p+ = 2Si/(Si + S2). For the limit S2 ^ Si we find the ideal open-end behaviour R = —1 and T = 0. The acoustic flow from pipe segment 1 cannot change the pressure in the much wider pipe segment 2, so that p+ + p– = 0. The outflow corresponding to a positive incoming pressure wave produces an under-pressure at the pipe outlet which propagates into the pipe as a reflected wave with negative amplitude wave. In the opposite limit S2 ^ S1, R =1 because the acoustic flux meets a closed pipe termination causing into a positive wave travelling back p+ — p– = 0, the result being that the pressure at the end of section 1 is twice as high. Hence, the transmission coefficient is T = 2. One can check by using the energy equation that this transmitted wave does not carry any energy in the limit S2/S;|_ ^ 0.