CHARACTERISTIC OR NATURAL MODES

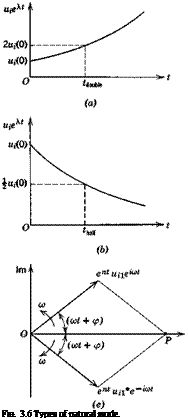
Solutions of the kind given by (3.3,14) describe special simple motions called natural modes or simply modes of the system. If the eigenvectors are orthogonal, the modes are normal or orthogonal modes. When A is real, the modes are exponential in form, as in Fig. 3.6a and 6—increasing in magni­tude for A positive, and diminishing for A negative. Thus A < 0 corresponds to stability, usually termed static stability in the aerospace vehicle context, and A > 0 corresponds to static instability, or divergence. The times to double or half of the starting value illustrated in the figure are given by

When one Ar is complex, for real matrices A, there is always a second that is its conjugate, and the conjugate pair, denoted (letting r = 1,2)

Aj,2 = П і І<0

define an oscillatory mode of period T = 2 tt/cd as we shall now show. The sum of the two particular solutions (3.3,14) corresponding to the complex pair of roots is

у = Ule(B+i0,)< + и2е(я-іш)<

where Uj and u2 are the eigenvectors for the two A’s. On factoring out ent we get

у = епі(щеіаі + и2е-іші) (3.3,26)

If the elements of the system matrix A are real, then the corresponding elements of Uj and u2 always turn out to be conjugate complex pairs, i. e.

u2 = uf

64 Dynamics of atmospheric flight and (3.3,26) becomes

у = eni(a cos cot + b sin cot) (3.3,27)

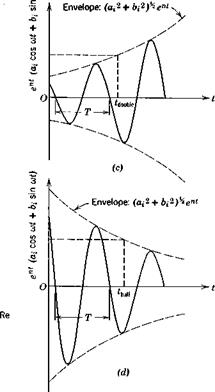
where a = Uj + uf and b = «(Uj — uj) are real vectors. Equation (3.3,27) describes, for any particular state variable yt, an oscillatory variation that increases if n > 0 (dynamic instability, or divergent oscillation) and decreases (damped oscillation) if n < 0—see Fig. 3.6c and d. The initial condition corresponding to (3.3,27) is

y(0) = a = ux + uf (3.3,28)

With reference to Fig. 3.6c and d, some useful measures of the rate of growth or decay of the oscillation are:

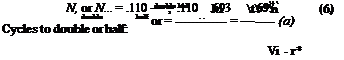Time to double or half:

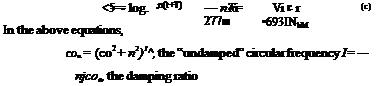
Logarithmic decrement (log of ratio of successive peaks):

One significance of the eigenvectors is seen to be that they determine the relative values of the state variables (the “direction” of the state vector in state space) in a characteristic mode. If the mode is nonperiodic, the eigen­vector defines a fixed line through the origin in state space, and the motion in the mode is given by that of a point moving exponently along this line. If the mode is oscillatory, the state vector is given by (3.3,27), and the locus of у is clearly a plane figure in the (a, b) plane through the origin. If n = 0, it is an ellipse, otherwise it is an increasing or decreasing elliptic spiral. The vectors a and b are twice the real and imaginary parts respectively of the complex eigenvector associated with the mode. It should be emphasized that these modes are special simple motions of the system that can occur if

the initial conditions are correctly chosen. In them all the variables change together in the same manner, i. e. have the same frequency and rate of growth or decay. It is instructive to consider the Argand diagram corresponding to (3.3,26). For any component y. L we have

y. = ent(uaei<oi + u*e-iat) (3.3,30)

which is depicted graphically in Fig. 3.6e, where ua = ua ё’ср. The two vectors are conjugate, i. e. symmetric w. r.t. the real axis, and rotate in opposite directions with angular speed w. The real value y^t) is given by their sum, the vector OP. As they rotate, the two vectors shrink or grow in length, according to the sign of n.

Once again it is necessary to consider separately the ease of repeated roots. Let us treat specifically the double root, i. e. m = 2 in (2.5,7). Then (3.3,14) is no longer the appropriate particular solution. Instead, we get from (2.5,7) a particular solution of the form

у (t) = ureV + vrte^f (3.3,31)

where ur and vr are constant vectors, ur being the initial state ur = y(0). On substituting (3.3,31) into (3.3,1), and dividing out eM, we find

{Xrur + vr) + Xrvrt = Aur + Av, f (3.3,32)

Since this must hold for all t, we may set t = 0, obtaining

(Arur + vr) = Aur

or vr = (A — ArI)ur

= —B(A>r Ф)

where В is given by (3.3,3), and (3.3,31) becomes

У(t) = (I – B(Ar)<)ureV (3.3,34)

After substituting (3.3,33a) in (3.3,32) a second relation is obtained, i. e.

Equation (3.3,31) will be a solution of (3.3,1) as assumed, if there exist a Xr and a vr that satisfy (3.3,35), and if ur given by (3.3,335) is not infinite. The first of these conditions requires that the original characteristic equation be satisfied, i. e.

It will now, because of the double root, be of the form

№ = (A – KfgW = 0 g(K) ф о (3.3,36)

and this condition is of course satisfied. The second condition is met by any eigenvalues found as described previously for repeated roots. Finally, the value of ur can be shown to be given by

= (-£ Т(ЯА (3-3,37)

dl ]x=xr

where v(A) is the column of adj В that gives the eigenvector vr.