Dynamic Similarity Principle

We already discussed geometrical similarity. In conducting experiments using scale models to determine force coefficients, it is clear that both the shape and orientation relative to airflow are important. However, suppose that we accurately measure the lift coefficient under conditions of geometric similarity on a model, for example, one-tenth the size of the actual vehicle. Is this enough? Can we now use this lift
coefficient to estimate the lift on the prototype? The results of Eq. 2.22 show that this might not work. We must conduct the test so that the Reynolds and the Mach numbers on the model match those on the prototype. If this is done, we will achieve dynamic similarity and the predictions most likely will work if we correctly identi­fied all of the key variables.

This is a concept of enormous value in the planning of experiments. Notice that even a complete theory or a complete numerical study often must be verified by experiments. It is therefore crucial to do this in a cost-effective and efficient manner. The principle of dynamic similarity is the key. In the wing-design example in the previous subsection, it is clear that if we had known the flight Reynolds and Mach numbers for the prototype, we would be able to design a test matrix that held these quantities fixed; the number of required test conditions could be reduced drastically.

It may not always be easy to match both the test Reynolds and Mach numbers to the prototype values. For instance, in testing a model of a hypersonic airplane, to fly at a Mach number of, for example, M = 11, configuring the test apparatus using a small model (no large wind tunnels can operate continuously in this Mach-number range) probably would lead to a Re that is too small to match that experienced on the full-sized prototype. However, it often may be the case that one or more of the similarity parameters is of lesser importance. In the hypersonic airplane example, it may be that dependence on viscous effects is secondary to compressibility effects, which are important in high Mach-number flight. Then, useful data still can be obtained without a matching Re. What is required here is an intimate knowledge of the sensitivity of the results to the parameters involved. This knowledge comes with experience. We attempt throughout this book to aid the student in acquiring at least some of the needed experience.

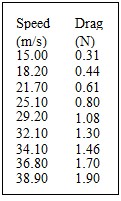EXAMPLE 2.4 Situation: A 1:10 scale model sailplane wing is tested in a wind tunnel to determine the aerodynamic characteristics. The span of the prototype is 15 m and the average chord (width) of the wing is 0.8 m. Sea-level air is the working fluid for both the model and full-sized wings.

Data from the test are shown in the table.

Required: (1) Sensitivity of the drag coefficient to the Re based on the average chord length; and (2) drag estimate for the prototype at a speed of 135 km/hr.

Approach: Use the dynamic similarity principle. If the drag coefficient can be shown to be insensitive to the Re, then the model data can be applied directly in estimating the drag.

Solution: The drag coefficient can be found from:

D

m

2P [6]mSm

where the subscript, m, refers to the model. Standard sea-level air has a density

0 8 15

of 1.23 kg/m3, and the area of the model wing is S = — x — = 0.120 m2.

m 10 10

which is dimensionally correct if the drag measurements are inserted in newtons (N) and the velocity is measured in m/s.

Because the kinematic viscosity for sea-level air is:

2

M. . _ . n-5 m v = — = 1.45 x 10 5 —,

P ^

the Re for the model based on the average chord is found from:

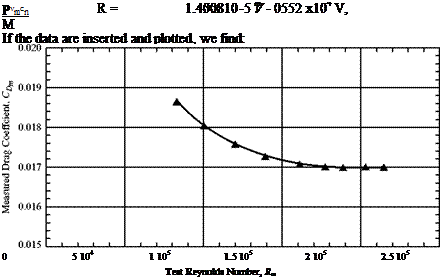
This shows that above a Re of about 1.5 x 105, the drag coefficient is insensi­tive to the Re (this may break down at yet higher speeds). This corresponds to a speed of about 27 m/s. Therefore, above this value, the drag coefficient has a nearly constant value of about CD = 0.017. If the prototype speed is: V

Appraisal: This example illustrates several useful features of the dynamic – similarity approach. It often happens that the aerodynamic force is insensitive to one or more of the similarity parameters. In this case, the Reynolds-number dependence was weak in the speed range of interest. Therefore, the drag coefficient measured in the wind tunnel could be used directly. Notice that there was no men­tion of possible Mach-number dependency; this is because the speed range is so low compared to the speed of sound that compressiblity effects are unimportant.