Elementary Flow Functions

If ф і and Ф2 are functions satisfying Equation 2.46 then, because this equation is linear, their sum will also satisfy Equation 2.46. In general, both the velocity potential and stream function can be constructed by summing less complicated functions.

Ф(х, у) = ‘2,фі(х, у) (2.53 a)

1-1

Ф(х, у) = фі(х, у) (2.53b)

І-l

Equation 2.53 represents the real benefit to be gained in describing a flow in terms of ф and ф. This statement will become obvious as the developments proceed.

The simple flows from which more complicated patterns can be

developed are referred to as elementary flow functions. There are three of them: uniform rectilinear flow, vortex, and source. The first of these has already been covered with ф and ф given by Equations 2.52 and 2.51, respectively.

Vortex

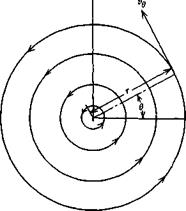
A vortex is pictured in Figure 2.13. This flow in two dimensions is purely circular around a point with no radial velocity component. Denoting the tangential velocity component by ve, the problem is to find ve as a function of r that will satisfy the set of Equations 2.43a and 2.43b. ve is to be independent of в.

In polar coordinates,

(2.54 a)

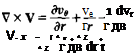(2.54b)

where r and в are the polar coordinates, with vr being the radial component of velocity and ve the tangential component.

Since vr is zero in Figure 2.13 and ve is independent of в, Equation 2.54b is satisfied identically and, from Equation 2.54a

or, after integrating,

rve = constant

У

Figure 2.13 Flow field around a vortex.

Thus, for potential flow, the tangential velocity around a vortex must vary inversely with the radial distance from the center of the vortex.

The strength of a vortex, denoted by y, is measured by integrating the tangential velocity completely around the vortex. The value of this integral is independent of the path providing it encloses the singular point at the center of the vortex.

y = <fcv-dR (2.55)

This closed-line integral of the velocity is known as the circulation. Evaluating Equation 2.55 on a constant radius leads to the relationship between the tangential velocity around a vortex, the radius, and the vortex strength.

Equation 2.55 is a well-known relationship and can be easily remembered from the definition of y.

ф and ф for a vortex follow immediately from Equations 2.50, 2.48, and

2.56.

If 6 is measured relative to zero and 6(B) is taken to be any value of 0,

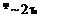(2.57)

The stream function for a vortex is found from

гв

= -^ln – 2 7T r(A)

Letting ф(А) be zero and r(A) be an arbitrary radius, a, leads to

* = – f

2 it a

The minus sign results from the choice of positive coordinate directions.

Source

The source is the counterpart of a vortex. Here the flow, pictured in Figure 2.14, is again symmetrical about the center, but it is entirely radial with no tangential velocity component.

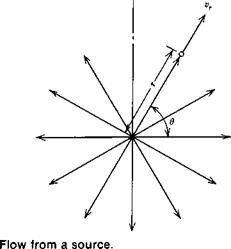The strength of a source, q, is measured by the total flux emanating from the center. From Figure 2.14, q is obviously given by

q = 2tTtvr

or

In a manner similar to that followed for the vortex, one may verify that for the source

ф=^-1пг (2.60)

2 tt

Equations 2.56 and 2.59, which define the velocities around vortices and sources, can be extended to three dimensions. If Q is the strength of a three-dimensional source, this flux will equal the product of the radial velocity and the surface area through which the velocity is passing. Thus, one can write vr immediately as

Q

4ттг2