Equations of Motion
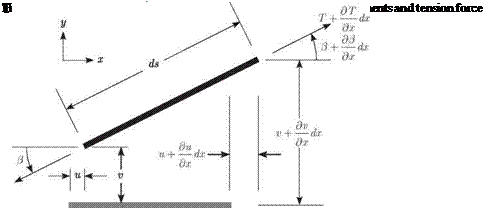
A string of initial length £0 is stretched in the x direction between two walls separated by a distance I > £0. The string tension, T(x, t), is considered high, and the transverse displacement v(x, t) and slope в(х, t) are eventually regarded as small. At any given instant, this system can be illustrated as in Fig. 2.1. To describe the dynamic behavior of this system, the forces acting on a differential length dx of the string can be illustrated by Fig. 2.2. Note that the longitudinal displacement u(x, t), transverse displacement, slope, and tension at the right end of the differential element are
represented as a Taylor series expansion of the values at the left end. Because the string segment is of a differential length that can be arbitrarily small, the series is truncated by neglecting terms of the order of dx2 and higher.
|
д ‘Г (аЛ d2u – [TcosOT] = m—г |
Neglecting gravity and any other applied loads, two equations of motion can be formed by resolving the tension forces in the x and y directions and setting the resultant force on the differential element equal to its mass mdx times the acceleration of its mass center. Neglecting higher-order differentials, we obtain the equations of motion as
where for a string homogeneous over its cross section
is the mass per unit length. From Fig. 2.2, ignoring second and higher powers of dx and letting ds = (1 + e)dx where e is the elongation, we can identify
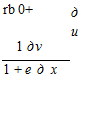
![]() (2.17)
(2.17)
Noting that cos2(e) + sin2(e) = 1, we can find the elongation e as
Finally, considering the string as homogeneous, isotropic, and linearly elastic, we can write the tension force as a linear function of the elongation, so that
T = EAe (2.19)
where EA is the constant longitudinal stiffness of the string. This completes the system of nonlinear equations that govern the vibration of the string. To develop analytical solutions, we must simplify these equations.
Let us presuppose the existence of a static-equilibrium solution of the string deflection so that
u(x, t) = u(x) v(x, t) = 0
в (x, t) = 0 (2.20)
e(x, t) = e(x)
T(x, t) = T(x)
We then find that such a solution exists and that if u(0) = 0
T(x) = To
ч T0 5 n 014
e (x) = "0 = EA = £ <2-21)
u(x) = e0x
where TO and e0 are constants and 5 = £ – £0 is the change in the length of the string between its stretched and unstretched states.
If the steady-state tension T0 is sufficiently high, the perturbation deflections about the static-equilibrium solution are very small. Thus, we can assume
u(x, t) = u(x) + U(x, t) v(x, t) = V(x, t)
e(x, t) = e(x, t) (2.22)
e(x, t) = e(x) + e(x, t)
T(x, t) = T(x) + T(x, t)
where the () quantities are taken to be infinitesimally small. Furthermore, from the second of Eqs. (2.17), we can determine в in terms of the other quantities; that is
![]() 1 dv 1 + e0 d x
1 dv 1 + e0 d x
Substituting the perturbation expressions of Eqs. (2.22) and (2.23) into Eqs. (2.15) while ignoring all squares and products of the () quantities, we find that the equations of motion can be reduced to two linear partial differential equations
„ .92U d2U
EA—- = m—г
![]() 9×2 dt2
9×2 dt2
T0 d2v d2v
1 + Є0 dx2 m d t2
Thus, the two nonlinear equations of motion in Eqs. (2.15) for the free vibration of a string have been reduced to two uncoupled linear equations: one for longitudinal vibration and the other for transverse vibrations. Because it is typically true that EA > T0, longitudinal motions have much smaller amplitudes and much higher natural frequencies; thus, they are not usually of interest. Moreover, the fact that EA > T0 leads to the observations that e0 < 1 and 5 < £0 (see Eqs. 2.21). Thus, the transverse motion is governed by
d 2v d 2v 70 dx2 = m 9f2
For convenience, we drop the ()s and the subscript, thereby yielding the usual equation for string vibration found in texts on vibration
![]() d 2v d 2 v
d 2v d 2 v
T—r = m—T – dx2 dt2
This is called the one-dimensional “wave equation,” and it governs the structural dynamic behavior of the string in conjunction with boundary conditions and initial conditions. The fact that the equation is of second order both temporally and spatially indicates that two boundary conditions and two initial conditions need to be specified. The boundary conditions at the ends of the string correspond to zero displacement, as described by
![]() v(0, t) = v(t, t) = 0
v(0, t) = v(t, t) = 0
where it is noted that the distinction between t0 and t is no longer relevant. The general solution to the wave equation with these homogeneous boundary conditions comprises a simple eigenvalue problem; the solution, along with a treatment of the initial conditions, is in Section 3.1.
2.2.1 Strain Energy
To solve problems involving the forced response of strings using Lagrange’s equation, we need an expression for the strain energy, which is caused by extension of the string, viz.
1 (t0 9
P =- EAe2dx (2.28)
2 Jo
where, as before
and the original length is t0. To pick up all of the linear terms in Lagrange’s equations, we must include all terms in the energy up through the second power of the unknowns. Taking the pertinent unknowns to be perturbations relative to the stretched but undeflected string, we can again write
€ (X, t) = Є(x) + € (X, t)
u(x, t) = u(x) + U(x, t) (2.30)
v(x, t) = v(x, t)
For EA equal to a constant, the strain energy is
EA C t0
P = (є2 + 2€€ + €2) dx (2.31)
20
From Eqs. (2.21), we know that T = T0 and є = €0, where T0 and €0 are constants. Thus, the first term of P is a constant and can be ignored. Because T0 = ЕАє0, the
strain energy simplifies to
Using Eqs. (2.29) and (2.30), we find that the longitudinal strain becomes
![]() л _ dU 1 fdv2
л _ dU 1 fdv2
Є дX + 2(1 + e0) V dx) +
where the ellipsis refers to terms of third and higher degree in the spatial partial derivatives of u and v. Then, when we drop all terms that are of third and higher degree in the spatial partial derivatives of U and 0, the strain energy becomes
![]() P=To Г £dx+2(тЬ f (ё)dx+^rj’* (ё
P=To Г £dx+2(тЬ f (ё)dx+^rj’* (ё
Assuming U (0) = її (£0) = 0, we find that the first term vanishes. Because perturbations of the transverse deflections are the unknowns in which we are most interested, and because perturbations of the longitudinal displacements are uncoupled from these and involve oscillations with much higher frequency, we do not need the last term. This leaves only the second term. As before, noting that e0 < 1 and dropping the о and subscripts for convenience, we obtain the potential energy for a vibrating string
![]()
![]() (2.35)
(2.35)
as found in vibration texts.
In any continuous system—whether a string, beam, plate, or shell—we may account for an attached spring by regarding it as an external force and thus determining its contribution to the generalized forces. Such attached springs may be either discrete (i. e., at a point) or distributed. Conversely, we may treat them as added parts of the system by including their potential energies (see Problem 5). Be careful to not count forces twice; the same is true for any other entity as well.












