Molecular Origin of Viscous Forces

The part of the interaction force parallel to the surface, dFt, often is described as the shear force or viscous force. As the latter term suggests, it is the result of frictional effects and is a major source of drag force on aerodynamic vehicles.

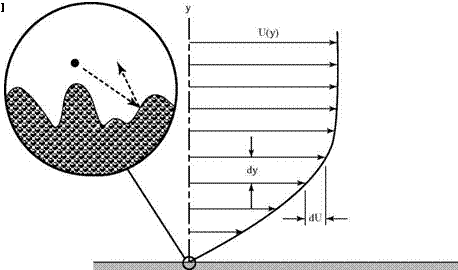
As in the case of the pressure, the simple ideas of kinetic theory based on random molecular motion provide a useful physical picture of the origin of shearing stresses in a fluid or a gas. The random motion tends to eliminate discontinuities that may form in a gas-velocity distribution. For example, consider the gas flow over a surface, as shown in Fig. 2.2. The parallel velocity distribution is expected to look somewhat like that shown in Fig. 2.3.

The molecules in the immediate vicinity of the surface must be brought to rest. The result is known as the no-slip condition and is satisfied in almost all practical situ­ations.[1] Gas particles lose momentum in the tangential direction at the surface due to collisions with the irregular-surface molecular lattice, as depicted in the blowup of a small region near the surface in Fig. 2.3. Clearly, if the mean free path is short, as it almost always is, there will be molecular collisions between the crystal-lattice structures of the surface (which, on the microscopic scale, represent a rough surface texture) involving lateral-momentum transfer. Gas particles must be brought to rest in the tangential direction at the surface.

Consider this simple thought experiment based on events leading up to the steady-state situation illustrated in Fig. 2.3. The surface is suddenly introduced into uniform flow parallel to the surface moving at velocity U. This initially creates a discontinuity in the velocity distribution because the no-slip condition applies only

to gas particles close to the surface. This discontinuity must be adjusted by the mol­ecular motion. Gas molecules at a distance have yet to be affected by the pres­ence of the surface. Molecules moving outward from the surface vicinity have zero momentum parallel to the surface. The mixing of these two types of molecules must finally produce a velocity distribution similar to that shown in Fig. 2.3. (It is the task of subsequent chapters to determine the exact form of this distribution.) The effect can be visualized as the dragging-along of slower fluid particles located closer to the surface by those at a greater distance, and a similar retardation of molecules farther from the surface by those that have been affected already by its presence. A careful measurement of the force on the surface would show that there is a shearing stress, t, that tends to move the plate in the original direction of the fluid. There is, of course, an equal and opposite retarding stress on the fluid.

If two layers of fluid separated by a vertical distance, dy, are considered, a change of velocity, dU, is evident between the layers, which can be interpreted as the net result of molecular mixing at that particular location. That is, it is a measure of the local shearing stress in the fluid. The force per unit area parallel to the surface, the shear stress, can be written asf

dU

dy

where the constant of proportionality is the coefficient of viscosity, ц. The region in which the adjustment of the velocity is made by molecular diffusion or mixing is called a boundary layer and is studied in a subsequent chapter. The value of the shearing stress, t, at the surface has the maximum value because the velocity gradient

f This equation often is referred to as Newton’s Law of Viscosity. Gases or liquids that behave as

indicated are called Newtonian fluids; those that do not are called non-Newtonian fluids and are rarely encountered in aeronautics.

is largest there. The viscosity coefficient, p, mainly depends on the temperature of gases; it also may be sensitive to pressure in other media.