Plan for Study of Aerodynamics

In the chapters that follow, we present the theory of aerodynamics mainly by means of a set of increasingly more realistic models of key flow phenomena. Chapter 2 discusses basic flow behavior and indicates strategies to represent the physical prob­lems in mathematical form. Each chapter contains many examples that illustrate the techniques for solving key problems. An important aid to learning the material is a set of computer programs that demonstrate application of the solutions and numerical approaches required in the solution of more complex situations. The problem set at the end of each chapter provides students the opportunity to develop their skill with the material.

Organization of Text Material

It is demonstrated in Chapter 2 that a convenient way to study aerodynamics is to organize it into a set of flow regimes, each of which focuses on an important special

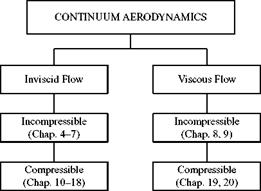
Figure 1.16. Organization of textbook material into flow regimes.

case governed by special features of the fluid motion. Chapter 3 is a review of the fundamental physics and modeling strategies needed to describe aerodynamic flows. These concepts are developed in the mathematical language needed to formulate and solve the key problems of aerodynamics.

Chapter 3 emphasizes the need for several methods of approach in problem formulation and solution. A major goal is to instruct the student regarding the cor­rect choice of the most effective strategies for problem solution. Features of real – life aeronautical situations calling for either analytical, numerical, or experimental approaches (or combinations of these fundamental problem-solving methods) are introduced throughout the book by using examples and the problem sets based on them.

Figure 1.16 presents the book layout in terms of the flow regimes, which are organized so that each part forms the foundation for those that follow. Thus, we begin in Chapter 4 to study problems that can be described in terms of a flow field that is both frictionless and incompressible. This leads to the simplest type of math­ematical formulation, which can be treated using many of the engineering math­ematics tools acquired in other courses. For instance, methods of linear differential equation theory, vector analysis, and integral theorems are applied in an elegant solution method usually referred to as potential-flow theory. This forms the basis for the solution of many problems of major importance in aeronautics. A key example is the treatment of flow around an airfoil, which leads to an understanding of the generation of lift—a central theme of aerodynamics.

The fluid-mechanics solutions are progressively extended to include problems that are affected strongly by compressibility and viscous effects. The former study leads us into the important flow regimes of transonic, supersonic, and hypersonic flight. Inclusion of viscous forces leads finally to a comprehensive model in which all important features of the flow about an object at any speed or any altitude can be accommodated. Numerical techniques are introduced to solve these problems when the complexity precludes an analytical approach.

In addition to the categories shown in Figure 1.16, we could add further unsteady and low-density or free-molecular flows in each regime illustrated. In this book, however, these latter types of problems do not have a central role.

PROBLEMS

1.1. Referring to the free-body diagram in Fig. 1.13, write the three equations for static equilibrium. Show that the center of pressure must coincide with the center of mass so that the system is in equilibrium flight.

1.2. Draw the free-body diagram of a glider in steady flight (i. e., constant velocity) in still air. Note that the velocity vector must lie at a downward angle, y, to the local horizon so that the force system is in equilibrium. By examining the com­ponents of the lift and drag, show that the tangent of this angle is proportional to the inverse of the L/D ratio. Also show that the ratio of the distance covered along the ground to the altitude lost is proportional to the L/D ratio.

1.3. Compare the gliding distance in still air of the following three airplanes if power is shut off at an altitude of 10,000 feet:

(a) Curtis Jenny with a glide ratio of L/D = 8

(b) Boeing 767 with a glide ratio of L/D = 14

(c) high-performance sailplane with a glide ratio of L/D = 55

1.4. If the measured range of a certain airplane in its aerodynamically unrefined form is 800 miles, what percentage reduction in the drag, D is needed if the range must be increased to 1,200 miles?

1.5. A small airplane is to be designed to fly nonstop around the earth. Describe some of the design features that you would incorporate. Then, compare your design to the Rutan Voyager that actually accomplished this task. Why does it look like a sailplane?

REFERENCES AND SUGGESTED READING

Anderson, John D., Fundamental Aerodynamics, McGraw-Hill Book Company, New York, 1984.

Crouch, Tom D., A Dream of Wings, Americans and the Airplane, 1875-1905, W. W. Norton & Co., New York, 1981.

Gabrielli, G., and von Karman, T, “What Price Speed?,” Mechanical Engineering, Vol. 72, 1950, pp. 775-781.

Hallion, Richard P., Supersonic Flight: Breaking the Sound Barrier and Beyond, The Smithsonian Institution, 1972.

Hirsch, Robert S., Schneider Trophy Racers, Motorbooks International, 1993.

Kinnert, Reed, Racing Planes and Air Races, Aero Publishers, 1967.

Yeager, J., and Rutan, D., Voyager, Alfred A. Knopf, Inc., 1987.