REPEATED ROOTS
When the procedure given in the foregoing is applied to calculate eigenvectors for cases of multiple roots of the characteristic equation, additional possibilities occur. (See refs. 3.3 and 2.2.) Let the multiple root occur at
« = X„
(i) If adj B(XB) is not a null matrix, then its nonzero columns give a single eigenvector, just as for distinct eigenvalues. In that case there is only one eigenvector for the multiple root.
(ii) If adj В(Я„) is null, and its first derivative djds adj B(s)|s=A]> is not, then there are two linearly independent columns of the latter that give two independent eigenvectors.
(iii) If the first derivative is also null, then higher derivatives will yield successively larger numbers of eigenvectors.
EQUATIONS IN NONSTANDARD FORM
It is not necessary, nor always more convenient, to work with the system equations in standard first-order form, as was done above. The characteristic equation can be found directly from the equations as they are initially formulated, the “natural” form. Consider (3.2,10) for example. The autonomous equations are
![]() (3.3,21)
(3.3,21)
Assume there is an eigenfunction solution like (3.3,14), i. e.
(3.3,23)
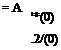 |
||
The square matrix of (3.3,23) is exactly the same as В in (3.2,13), A replacing s. Since (3.3,23) are homogeneous equations the determinant of В must be zero. Expanding it leads exactly to the correct characteristic equation, just as would be obtained from the standard first-order form. Equation (3.3,23) is of the same form as (3.3,156) and the same argument for finding an eigenvector applies—i. e. a column (z(O), y(0)) that satisfies (3.3,23) is any non vanishing column of adj B. To complete the eigenvector we need x(0) and 2/(0). These are simply, from (3.3,22),
where A is the appropriate eigenvalue.











