Resonators in duct systems

Acoustic energy can accumulate in parts of a duct system delimited by strongly reflecting boundaries, an example of this being an expansion cham­ber of length L and cross section Sm along a pipe of cross section Sp << Sm. Such an expansion chamber can also be used as muffler, to reflect waves generated by an engine. Maximum transmission losses are found in cases where the expansion chamber length matches an odd number of quarter wave-length of the incoming waves (figure 13). Other obvious examples of resonators are pipe segments terminated either by open or closed pipe ter­minations.

The flute can be approximated as an open-open pipe with uniform cross section displaying resonances when an integer number of half wave length matches the pipe length. Since the mouth opening of the flute is smaller than the pipe cross section, the end correction of the mouth opening is quite large. This implies an important inertia, which would detune the pipe resonances if it was not combined with a compliance approaching that of a pipe segment of the length of the end correction. For this reason the mouth of the flute is not at the pipe termination. The volume in the dead end between the closed pipe termination and the mouth opening is adjusted by means of a movable piston (cork) so that the first resonances of the pipe are exactly multiples of the fundamental. This strongly enriches the sound produced by the instrument [Chaigne and Kergomard (2008)].

The close-open pipe of a uniform cross-section is a model for the clarinet. It displays resonances when the length of the pipe matches an odd number of quarter wave-length. This promotes odd harmonics of the fundamental, giving the sound a particular character. The use of a conical close-open pipe, such as the oboe or the saxophone, provides a series of resonances at frequencies that are a multiple of half wave length matching the pipe

• Experiments — Theory

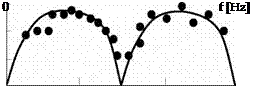
Figure 13. Comparison between measurement [Davis 1954] and theory [Dowling 1983] for transmission losses of a simple expansion chamber along a pipe with an anechoic termination. The transmission losses are defined by: TL = 20log(I/T), with I the amplitude of the incident wave and T the amplitude of the transmitted wave. Maxima of transmission losses corre­spond to a length equal to an odd number of quarter wave-length. Minima correspond to an integer number of half wave-length.

length. In conical pipes the acoustic field is dominated by spherical waves rather than plane waves. Consequently the radiation efficiency of the sound source (reed) increases at low frequences linearily with the frequency, as demonstrated by equation (63). Thus, contrary to the clarinet, the low­est resonance frequency does not correspond to the strongest impedance in conical pipe instruments [Chaigne and Kergomard (2008)].

A pipe system can display localized acoustic standing waves, captured between two reflectors. A typical reflector is a closed side branch and the closed end of it imposes a standing wave within the side branch [Bruggeman et al. (1991), Ziada and Buhlmann (1992), Tonon et al. (2011)]. The incom­ing and reflected waves have equal amplitudes as imposed by the closed pipe termination R =1. Whenever the closed side-branch length corresponds to

an odd number of quarter wave-length the standing wave imposes a pres­sure node at the junction of the closed side branch with the main pipe. At low frequencies the pressure is continuous over the junction and this imposes a pressure node in the main pipe (equation 157). Thus, this pres­sure node acts as an ideal open pipe termination with R = —1. When two closed side branches with equal resonance frequency are placed at a distance corresponding to an integer number of half a wave length, we ob­tain an acoustically perfectly closed system [Bruggeman et al. (1991), Ziada and Buhlmann (1992), Tonon et al. (2011)]. Paradoxically enough, this system is open for the flow [Hein and Koch (2008)]. The most spectacular resonances are obtained when considering two opposite closed side-branches forming a cross configuration with the main pipe [Keller (1984), Kriesels et al. (1995), Dequand et al. (2003c), Slaton and Zeegers (2005)]. This will be discussed in more detail in the next chapter.

A series of closed side branches of equal length can display strong acous­tical resonances even if the side-branches are placed at arbitrary distances from each other. A system of deep closed side branches of random depth can also display Anderson localization [Depolier et al. (1986)].

Another example of strong localization of a resonant acoustic field in an apparently open system is the Beta Parker mode in a pipe system with a splitter plate [Welsh and Stokes (1984),Stokes and Welsh (1986)]. When the longitudinal splitter plate (separating the pipe in two equally wide parallel ducts) is longer than the pipe width, there is a resonance for which the half wave length is longer than the pipe width. Hence, at this frequency only plane waves propagate along the main pipe. If the two pipe segments separated by the splitter plate are oscillating in opposite phases, the system will not radiate any plane waves and actually does not radiate at all. This type of resonance has been observed in ventilation ducts (due to guiding vanes at bends), turbines (stator or rotor) [Welsh and Stokes (1984), Stokes and Welsh (1986)] and even protection grid in building (ventilators, roof) [Spruyt (1972)].