APPLIED LIFTING-LINE THEORY

One of the most useful tools in the aerodynamic de­sign of airplanes is the lifting-line wing theory, first pub­lished in 1918 (l, a). Practical results and limitations are presented as follows.

VORTEX SHEET (3). As explained in the chapter dealing with the characteristics of “airfoil sections”, lift is the result of a “bound vortex” or “lifting line”. In wings with finite span, the circulation around this line does not discontinue at the ends or tips. Imme­diately behind the line, a vortex sheet with a more or less uniform downward velocity V leaves the wing. As a consequence of the pressure difference between lower and upper side of the lifting surface, a certain flow is caused around the lateral edges, thus starting a pair of strong trailing vortices. The vortex sheet immediately begins to roll itself up into these vortices; and it even­tually passes all of its vorticity into the pair shown in part (b) of figure 1. Note that the sheet also contains the viscous wake (boundary layer) of the wing. The “dead” air rolls “into” the trailing vortices together with the vorticity. Ц is not correct, however, to assume, that the viscous wake would be sucked into the vortex cores. More information on shape and location of the vortex sheet is given in “longitudinal stability”.

TRAILING VORTEX. The structure of a vortex is de­scribed in the “general” chapter. The size (diameter) of the viscous core depends upon viscosity and upon the disturbance (separation) of the flow at the edge from which it originates. For example, in chapter VII of “Fluid-Dynamic Drag”, the diameter of a core starting from a rounded lateral edge is seen to be d.— 0.05 c, where c= chord length of a rectangular wing, with A = 3, at Сц~0.6. As reported in (2,c) the diameter is proportional to Cjj and it is a function of scale (Rey­nolds number). As measured in flight (at R^ = 3( 10)^, and CL— 0.75) the diameter was found to be 10% of the wing-tip chord, while in a wind-tunnel test at Rc = 2( 10) it was about twice as large. At a distance behind the trailing edge x= c, where these tests were performed, the pressure within the viscous core is in the order of Cp= — 1. The diameter grows with distance. For ex­ample, flight tests (3,c) indicate for a wing with A = 6, at CL= 0.9, a core diameter d = 0.2 b, at x ~ 25 b.

ROLL-UP. As observed in wind-tunnel tests, the tip vortices start forming at the corner of the leading edge (if there is one, as in rectangular or tapered wings). Theoretically (for elliptical lift distribution across the span) the final distance between the vortex centers is bjfb = тг/4. As indicated in (2,b) the distance x as de­fined in part (a) of figure 1, is

x/b = 0.1A/Cl= 0..1/CLb (0)

where CLb=L/qb. As derived in (16,a) the distance from the lifting line where the roll-up is “completed”, is approximately

x/b = k/CLb (1)

where к = 0.4, for “essentially” rolled-up condition; and к •= 0.9, indicating that 99% of the vorticity is concen­trated in a pair of non-viscous cores. Nominally, the diameter of these cores isd=?b(2/3). For example, for C|j=- 1, and A = 5, and CLb= 0.2, the 99% rolled-up distance is x = 4.5b, orx = 22c. However, at or be­yond this distance, dissipation takes over. Nevertheless, as pointed out in (2,a) the vortices generated by a trans­port plane with W = 300,000 lb, and b =. 43 m, flving at Cl=1.2 (climbing) corresponding to V=160 kts, still persist after more than 2 minutes, at a distance behind the aircraft of 10 km (!). In this manner, such an air­plane leaves behind a disturbance with up and down velocities up to plus/minus 3 or 4 m/s. Another airplane, flying into this wake, can then encounter angle-of-attack differentials in the order of plus/minus 2 or 3° , and local lift differentials in the half wings, up to plus/minus 15%.. A smaller airplane hitting the center of a vortex, might even be rolled over.

RECTANGULAR WINGS. Most analyses consider el­liptical lift distribution. For sharp or square-ended rec­tangular wings, experimental evidence such as in fig­ure 10, suggests a vortex span in the order of b[==. 0.9b. It seems that the lateral edges of such a planform are a continuation of the bound vortex, thus making this shape more effective and efficient than predicted by the “chordless” theory. In fact, when assuming the lateral edges to be end plates (see later) reasonable answers are obtained for induced angle and effective aspect ratio (equation 2).

DOWNWASH. An integral part of the flow pattern be­hind a lifting wing is a permanent downward deflection (downwash) of the affected stream of air. Lift can thus be understood as the result of that deflection. In wings with an elliptical distribution of lift or load along the span, the affected stream is equal in magnitude I but it is not identical) to that contained in a cylinder having a diameter equal to the wing span ‘b Considering an air­plane in level flight, we may visualize this cylinder as being deflected so that it assumes the downward velocity V. Behind the airplane, the cylinder is thus inclined against the horizontal at the downwash angle s === w/V, until it finally meets the ground. There, the momentum imparted by the airplane upon the cylinder of air, is transferred onto the earth in the form of pressure. In this manner, the airplane may thus be considered as being supported from the ground.

INDUCED ANGLE. At the location of wing or lifting line, the average angle of deflection is but one half of that of the assumed cylinder at a sufficiently great dis­tance behind the wing. The angle at the wing is called “induced” (4). The minimum of the induced angle is theoretically found for elliptical distribution of the lift over the wing span:

= L/qirl? = С^АгАл (2)

where Ajdenotes the effective aspect ratio as explained later. This angle has to be added to that required in two – dimensional flow (as shown in the chapter on “airfoil sections”) to develop a certain lift coefficient.

LIFT ANGLE. The lift-curve slope of an airfoil in two – dimensional flow is theoretically dCb/dc<^=r 2тг. In­stead of this slope, it is more convenient, however, in practical applications of lifting-line theory, to use the reciprocal value dc</dC^ which shall be called the “lift angle”. Including the induced component, this angle is (in larger aspect ratios)

dcx/dCL = 1 /(2 a if) + l /( tAj) (3)

where subscript ‘2’ denotes th/angle in 2-dimensional flow. For conventional foil sections in undisturbed flow, the factor ‘a’ is in the order of 0.9. Using this value, equation (3) can be written in degrees, roughly as

do?/dCL= 1(H-(19/Aj) 10-И20/А) (4)

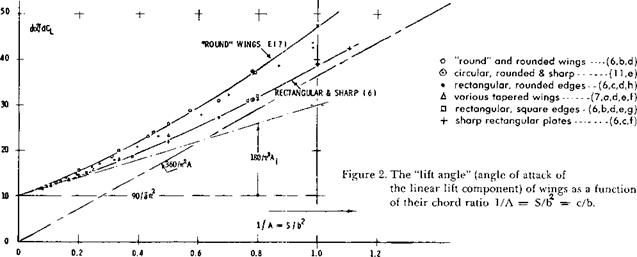
where T9’ and ‘20’ are somewhat larger than the theoret­ical minimum (180/тґ[36]) = 18.3°. This equation, rep­resenting lifting-line theory* is primarily applicable to wings with short chords, that is, with high aspect ratios A = b/c =- bS/S, where the average chord c = S/b. Accordingly, the function is seen in figure 2, adequately describing the lift angle of rectangular and/or moder­ately tapered wings, with sharp or square lateral edges, up to 1/A =■ 0.15, or down to A = 7.

“LIFTING SURFACE”. A wing is not a “line”. The chord has a certain influence upon the magnitude of the lift angle. As explained in the “small-aspect-ratio” chapter, a long chord appears not only in the form of a small ratio, but also in a three-dimensionality of the airfoil section used. On the basis of experimental results (9) in figure 2, the additional lift angle of the section, is

A(dof/dCL) = 9/A[37] (5)

Summing up, the lift angle of efficient wings is

do<p/dCL= 10 4- (9/A2) – t – (20/A) (6)

This equation describes rectangular and moderately tapered plain wings with sharp or square lateral edges.

(3)

Regarding rolling-up trailing wing-tip vortices:

a) Bird, Visualization, J Aeron Sci 1952 p 481.

b) Hoerner, Tunnel Tests, see (13,a, b,f).

c) Kraft, Flight Tests, NACA TN 3377 (1955).

d) Shape of vortex sheet behind delta and swept wings, see NACA TN 3175 (1954) 8c 3720 (1956).

e) Vortex Wakes, RAE TN Aero 2649, and ARC CP 795.

f) ARC, Flight Tests, CP’s 282,489,795 (1954/65).

(4) The word “induced” refers to an analogy to the magnetic field around a wire carrying electric current. Glauert: “induced velocity at any point corresponds to magnetic force due to current”.

(6) Systematic investigations of rectangular wings:

a) Series of Wings, Service Technique No. 83.

b) Gottingen, Rectangular, Ergebnisse I, III 8c IV.

c) Winter, Plates and Wings Short Span, Forschung 1935 p 40 8c 67; Translation NACA T’Memo 798.

d) Zimmerman, Various Shapes, NACA Rpt 431 (1932); also Circular, TN 539 (1935); J A Sci 1935 p 156.

e) Higgins, In VD Tunnel, NACA T’Rpt 275 (1927).

f) Wadlin, Hydrodynamics of Rectangular Plates, NACA TN 2790, 3079 8c 3249, or T’Rpt, 1246 (1955).

g) Scholz, Forschung Ing’Wesen 1949/50 p 85.

h) Brebner, Various Wings, RAE Rpt 65236 (1965).

i) Bussmann, 0015 Wings, ZWB T’Berichte 1944 p 245.

(7) Lifting characteristics of tapered wings:

a) Anderson, Investigation of 22 Tapered Wings,

NACA TR 572 8c 627 (1936/38); also T’Rpt, 665′(1939).

b) Junkers Wind-Tunnel Results, about 1941.

c) Truckenbrodt, Delta Wings, ZFW 1956 p 236.

d) Allen, 3 Tapered on Fuselage, NACA RM A53C19.

e) NACA; A =- 8, 10, 12, TN 1270 and 1677 (1947/48).

f) Wolhart, A = 2 to 6, NACA TN 3649 (1956).

g) King, Taper Ratio Series, NACA TN 3867 (1956).

(8) Distribution of lift across the wing span:

a) Multhopp, Calculation of Distribution Across Wing Span, Lufo 1938 p 153 (Transl ARC No. 8516).

b) DeYoung, Arbitrary Plan Form, NACA Rpt 921.

c) Schrenk, Simple Procedure, Luftwissen 1940, p 118; English translation, NACA T’Memo 948.

d) Hafer, Improvement of (c), Luftwi 1944 p 12.

e) Laporte, Examination of (c), J A Sci 1955 p 787.

(9) We do not agree with the widely used form­ulation (12,a) whereby the angle as in equation

(5) is in the order of A(do8/dCj_) — 8/A.

“ROUND” WINGS are meant to have rounded lateral edges and/or to be rounded in the planform (see later) of the wing “tips”. As a consequence of some flow around the lateral edges, not only the effective aspect ratio, but also the effective wing area is reduced. To properly formulate these effects would be complex. The experimental results in figure 2, suggest, however, as an upper limit:

dcx°/dCL = 10 + (12/A2) + (25/A) (7)

It is not certain that the last term of this equation rep­resents induced drag only. In fact, when A reduces by ДА to Aj, the effective area can be assumed also to be reduced, thus increasing the sectional angle of attack required. Equations (6) and (7) demonstrate that the components of the angle of attack can be added to each other. In the case of wind-tunnel tests and/or in the presence of the ground, the correction of the angle of attack caused by the boundaries of the fluid space, presents another angle-of-attack component. For those who wish to think in terms of lift-curve slope, equation (3) transforms into

dCL/do/ = 2air/(l + 2a/A-L) (8)

where (2 aT) =■ lift-curve slope of the foil section used (as in two-dimensional flow). Transformation of equa­tions (6) and (7) would be complex.

DIHEDRAL is the academic word for what we can also call “V” shape. Lifting-line theory as described in this section, has one final application in such wings. As pointed out in (14,a) when raising the tips of a straight wing (thus reducing the span), each wing panel approximately maintains induced characteristics, in the plane normal to the panel, equal to those of the original straight wing. The lift of a panel (in verti­cal direction) is equal to (normal force) times (cos/*)- Since the angle of attack is measured in the wing’s plane of symmetry, the lift angle (X^of a dihedraled
wing is expected to be

dot/dC^ =■ (0.5/тґсо s*f) + (l/trAp cos2D (9)

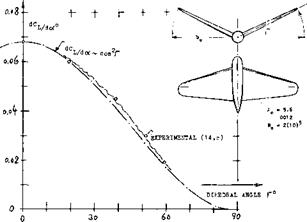
where ‘p’ indicates that the reference area is the sum of the panel areas, Sp , and Ap – 2 s/c ж 4 sVSp, where s = span of a panel, = 0.5 b. As confirmed by the experimental results on a “V” shaped tail sur­face in figure 3, lift then reduces in proportion to cos2Г. The lateral force derivative of the surface is shown in the chapter on “directional stability and control”.

Figure 3. The lift coefficient (based on sum of panel areas) of a “V” tail surface, as tested (14,c) and as calculated (14,a) as a function of the dihedral angle.

INDUCED DRAG. Referring the lift coefficient of a dihedraled wing to the projected planform area S = b c, it is found that CNp, where ‘p’ indicates that the normal force is still referred to the panel area. Equa­tion (9) then changes into

do(/dC^=z (0.5/trcosD 4- (1/trA cos ) (10)

Defining now A — b/c, the induced lift angle is

doq/dCL= SArb2 (n)

where S = projected area, as above. – For a dihedral angle of 6°(as possibly used in the wings of conventional airplanes) the increment is expected to be only in the order of 1%. However, “V”-shaped tail surfaces have been used in place of the conventional tail assembly, with dihedral angles in the order of 30. Comparing such a surface with a straight horizontal tail having the same span, equation 11 predicts that induced angle and induced drag will remain unchanged. A more correct analysis (14,b) indicates the very small decrease as shown in figure 21. For example, at Г-30 , the reduction (when keeping b = constant) is in the order of 4%.