. RESPONSE TO A SET OF STATIONARY RANDOM INPUTS

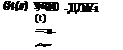We now consider the case when the system response is a sum of responses to a set of random inputs. An example of this situation is the roll response of an airplane flying through a turbulent atmosphere, when there is a multiple input associated with the three components of the atmospheric motion, each contributing to the output via a different transfer function. Figure 3.21 shows an example in which a number of inputs combine to form a single out­put. More generally, for n inputs and m outputs related by an (m x n)

Fig. 3.21 Response to a set of random inputs.

transfer function matrix G(.s)

f(s) = G(.s)x(s)

By virtue of (3.2,2a) the transfer function matrix likewise connects the Fourier transforms of the inputs and outputs,

Y(m) = G(ico)X((») (a) (3.4,46)

or with reference to truncated functions, see (2.6,19),

Y(со; T) = G(*w)X(ft>; T) (b)

Now the cross-spectral density of two components (yi and yfl of у is given by

(2.6,22)

The matrix of Ф,, „ is therefore

Уг *з

Фу = lim — Y*(co; T)YT((o; T)

y-oo 4cT

= lim — [G(wo)X(co; T)]*[G(io>)X(o); T)]T т->ж 4:T

= lim — G*(ico)X*(co;T)XT(co; T)GT{iw) У->оо 4:T

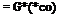
lim — X*(«; T)XT(w; T) 1 GT(im) y-oo 4T

From (3.4,48) it follows that the power spectral density of yt (a diagonal element of Фу) is

Ф, ЛМ =22 (3-4,49)

fc=l 1=1

and that if the input cross spectra are zero

ФздМ = І І^МІ*ф^ю) (3.4,60)

к=1

This is a very important result for application to flight dynamics since it provides a way of calculating the output power spectral density from a knowledge of all the input cross spectra and the relevant transfer functions. An important special case is that in which there is only one input, x(t) and one output, y(t). Then (3.4,50) reduces to

Ф„(«) = |£(»<у)12ФетМ

This is the most commonly used input/output relation for random processes. It will be recalled (see Sec. 2.6) that most of the interesting probability properties of y(t) can be deduced from Ф„(«).

A USEFUL THEOREM CONCERNING MEAN-SQUARE RESPONSE

In some calculations, it is not required to have the spectrum of the output, its mean-square value being all the information wanted. In such cases the desired result may be obtained more simply than by first calculating Фуу and then integrating it. The method is given in ref. 3.12 for single and dual inputs. We present below only the theorem for a single input.

Let the system, with transfer function G(s), be subjected to a transient input x(t), with corresponding transient output y(t). The integral square of the output is given by Parseval’s theorem (see ref. 2.4, Sec. 120).

Л 00 1 Л 00

E = y2(t)dt = — Y*(a>)Y(a>) day (3.4,52)

Jo 277 J-oo

where Y(a>) is the Fourier transform of y(t). Now the Fourier transform of the output is given by (3.2,2a) as

Y(o>) = G(iw)X(m)

and hence

E = — f” G(ia))G*(ico)X((o)X*(a>) dco 277 J—oo

1 Л00

= — G(ico)*X(co)2dco (3.4,53)

277 J—oo

Now we also have from (3.4,51) that if the input is a random function, the mean-square output is

__ Л 00

Уг = фет(«>) d°>

J—OO

=J G(ia))2<&xx(co)d<o (3.4,54)

By comparing (3.4,53) and (3.4,54), we see that у2 = E if

2т7фет(ю) = |X(o)|2 (3.4,55)

That is, if one can find a transient x(t) whose Fourier transform is related by (3.4,55) to the power spectrum of the given random function, then y2 can be calculated from the output of the transient. This may prove to be a much easier and more economical computation, whether an analog or digital com­puter is used. In particular, for spectrum functions like those of atmospheric
turbulence (the “Dryden” spectra) the following are suitable transients:

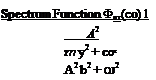Equivalent transient x(t)

Ае~Уг (3.4,66)

277 (a2 + <x>2)2

The advantages for analog computation are that no random function generator is needed, and that the computation using a single transient input takes much less time.