SUPERPOSITION THEOREM (CONVOLUTION INTEGRAL, DUHAMEL’S INTEGRAL)
The theorem of this section facilitates the calculation of transient responses of linear systems to complicated forcing functions. The general response appears as the superposition of responses to a sequence of steps or impulses which simulate the actual forcing function.
Let Xj(s) be the transform of xft)
![]() x2(s) be the transform of x2(t)
x2(s) be the transform of x2(t)
Then the function x3(t) whose transform is the product x3 = XjX2 is
![]() x3{t) = Г xfr)x2(t — t) dr
x3{t) = Г xfr)x2(t — t) dr
![]() Jt=0
Jt=0
/*00 /*00 x3 = e~suxflu) du X e~svx2(v) dv Jo Jo where и and v are dummy variables of integration. This is equivalent to the double integral
x3(s) = JJ*e~s(u+v)xl(u)x2(v) du dv s
 |
 |
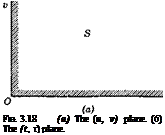
where 8 is the area of integration shown in Fig. 3.18a. Now let the region of
integration be transformed into the t, т plane by the substitution
U + V = t V = T
![]() x3(s) = Jj’e~sixft — т)ж2(т) dS’
x3(s) = Jj’e~sixft — т)ж2(т) dS’
S’
where S’ is the region shown in Fig. 3.186. Integration first with respect to
T §iVeS ЛОО M
x3(s) = e~st dt xflt — t)x2(t) dr Jt=o Jr=о
Therefore, by definition (2.3,7)
![]() rt
rt
Q. E.D.
 |
||
We now apply this result when the system G{s) is subjected to an arbitrary input x(t). The response is given by
The preceding equation applies to a single input/output pair. For a multivariable system we would obviously have as the extension of (3.4,40a) (and similarly for 3.4,406)
|
Vi(t) = |
f 2 M* — t)xAt) dr |
(a) |
||
|
} t—0 з |
(3.4,41) |
|||
|
or |
у (<) = |
I H(t — t)x(t) dr Jr=0 |
(b) |
where H is the rectangular matrix of impulse response functions.
By considering a slightly modified form of (3.4,39) we can obtain a companion result involving srf(t) instead of h(t). We may write (see 3.4,186)
y(s) = ^ • sx(s)
s
= s#(s){£P[x + ж(0)}
= s&(s) Л?[х] + stf{s)x{ 0)
Again applying (3.4,38) we get
![]() y(t) = j</(t)x(0) + Г stf(t — t)x(t) dr (a) Jr=о
y(t) = j</(t)x(0) + Г stf(t — t)x(t) dr (a) Jr=о
or y(t) = stf(t)x{0) + Г s/(r)x(t — t) dr (6)
Jr=0
As with the impulse response, the matrix form of (3.4,42a) for example, for a multivariable system, is
У(<) = **Z(t)x(0) + Г — t)x(t) dr (3.4,43)
Jr= о
SOLUTION INCLUDING INITIAL CONDITIONS
The general solution of (3.2,21) for arbitrary y(0) and arbitrary x(t) is obtained by superposition of the complementary function (3.4,17) and the “particular integral” (3.4,41 or 43). Thus in general
![]()
![]()
![]() (3.4,44)
(3.4,44)
The physical significance of (3.4,40a) and (3.4,42a) for example is brought out by considering them in the one-dimensional case as the limits of the following sums
y(t) = ^h(t~ t)x(t) At (a)
y(t) = stf(t)x{0) — t)x(t) At (b) (3.4,46)
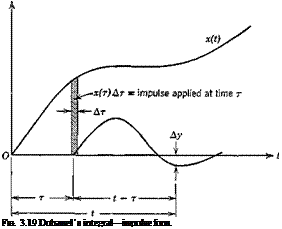 |
Typical terms of the summations are illustrated on Figs. 3.19 and 3.20. The summation forms are quite convenient for computation, especially when the interval At is kept constant.











