The conservation of energy

Conservation of energy implies that changes in energy, heat transferred and work done by a system in steady operation are in balance. In seeking an equation to represent the conservation of energy in the steady flow of a fluid it is useful to consider a length of stream tube, e. g. between sections 1 and 2 (Fig. 2.6), as

Fig. 2.6 Control volume for the energy equation

constituting the control surface of a ‘thermodynamic system’ or control volume. At sections 1 and 2, let the fluid properties be as shown.

Then unit mass of fluid entering the system through section will possess internal energy cyT, kinetic energy vj2 and potential energy gz, i. e.

(cvT + (2.9a)

Likewise on exit from the system across section 2 unit mass will possess energy

(cvT2 + у + gz^j (2.9b)

Now to enter the system, unit mass possesses a volume l/pi which must push against the pressure pi and utilize energy to the value of p x 1/pi pressure x (specific) volume. At exit P2/P2 is utilized in a similar manner.

In the meantime, the system accepts, or rejects, heat q per unit mass. As all the quantities are flowing steadily, the energy entering plus the heat transfer must equal the energy leaving.[5] Thus, with a positive heat transfer it follows from conservation of energy

rr. vf pi _ , V? P2 ,

cvT +-^4—— -gz +q = cvT2 + ^H——- hgz2

2 pi 2 p2

However, enthalpy per unit mass of fluid is cyT+р/р = cpT. Thus (cpT2 + у + gzij ~ (cpT + ^ + gz^j = q or in differential form

i(c, r + y + sS«,5a)=g (2.10)

For an adiabatic (no heat transfer) horizontal flow system, Eqn (2.10) becomes zero and thus

y2

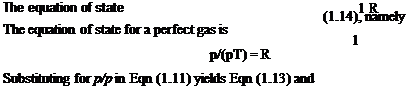cpT + — = constant (2-11)

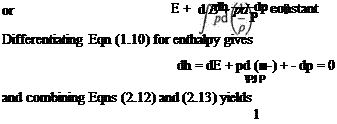The first law of thermodynamics requires that the gain in internal energy of a mass of gas plus the work done by the mass is equal to the heat supplied, i. e. for unit mass of gas with no heat transfer

But

Therefore, from Eqns (2.14) and (2.15)

=°

which on integrating gives

In p + 7 In ( — = constant

PJ

or

p = kp<

where к is a constant. This is the isentropic relationship between pressure and density, and has been replicated for convenience from Eqn (1.24).

The momentum equation for an incompressible fluid

Provided velocity and pressure changes are small, density changes will be very small, and it is permissible to assume that the density p is constant throughout the flow. With this assumption, Eqn (2.8) may be integrated as

ft? + ^ pv2 + pgz = constant

Performing this integration between two conditions represented by suffices 1 and 2 gives

i. e.

P +^pv I + pg= 1 = P2 +^pv22 + pg=2

In the foregoing analysis 1 and 2 were completely arbitrary choices, and therefore the same equation must apply to conditions at any other points. Thus

1 ?

p + – pv~ + pgz = constant

This is Bernoulli’s equation for an incompressible fluid, i. e. a fluid that cannot be compressed or expanded, and for which the density is invariable. Note that Eqn (2.16) can be applied more generally to two – and three-dimensional steady flows, provided that viscous effects are neglected. In the more general case, however, it is important to note that Bernoulli’s equation can only be applied along a streamline, and in certain cases the constant may vary from streamline to streamline.