The Helmholtz resonator

The bottle or Helmholtz resonator is an elementary acoustical resonator [Dowling and Ffowcs Williams (1983), Pierce (1990), Rienstra and Hirschberg (1999)]. It is an acoustical mass-spring system, because the volume of the bottle acts as a spring, while the inertia of the flow (mass) is concentrated in the neck (Figure 6.6). If the neck has a uniform cross section S and a

length L the mass obviously is:
M = p0S(L + 25)	(181)
Ap AV _ S Ax
(182)
where Ax is the acoustic fluid displacement in the neck. The uniform density assumption is actually in agreement with the fact that we neglect inertia in the volume of the bottle, implying a uniform pressure. This is exactly the same assumption as for a massless spring, which implies that the tension is uniform over the spring. Assuming an adiabatic compression we have: Ap = c2Ap. The force acting on the fluid in the neck is therefore:
AF = SAp	(183)

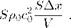
From this we deduce that the spring constant K of the system is:

K 2S2

K = Poco -у

and the resonance frequency of the resonator is given by:

= (185)

It is interesting to note that for an ideal gas poc0 = jp0 where 7 is the Poisson ratio of specific heats at constant pressure and volume respectively. When considering an oven or furnace with an open door, the gas density in the neck of the system is close to that of the surrounding air at room temperature, while the average pressure p0 in the volume is atmospheric. Hence, the resonance frequency depends only weakly on the temperature in the oven.

A bottle of cider or champagne has a neck with a non-uniform cross section S(x). In order to calculate its resonance frequency we need a more sophisticated approach [Cummings (1972)]. We start again by applying the integral mass conservation law on the volume, assuming a uniform density in the volume:

Pou’S (L)

where u’ is the acoustic velocity at the pipe opening x = L. Furthermore, we use the integral of the momentum equation (45) over the neck of the bottle:

where we assumed the flow in the neck to be incompressible. Elimination of u’ yields a second-order harmonic equation corresponding to the resonance frequency:

^0 = C0

with: