Thrust Approximations

Based on steady linearized aerodynamics, the local blade lift coefficient can be written as

Ci = Cta(a – a0) = С[а(в – «о – Ф), (3.19)

where Cia is the 2-D lift-curve-slope of the airfoil section(s) comprising the rotor, and «о is the corresponding zero-lift angle. For an incompressible flow, C/e would have a value close to the thin-airfoil result of 2n per radian. Although C/a will take a different value at each blade station because it is a function of local incident Mach number and Reynolds number, an average value for the rotor can be assumed without serious loss of accuracy (i. e., C/a = constant). Also, unless otherwise stated, it will be assumed that «о can be combined into в.

Therefore, C[a can be taken outside of the integral sign giving

cT = f Cir2 dr = aCi« f (0 – ФУ2 dr>

^ Jo 2 Jq

and using the result that ф = к/r, then the thrust coefficient can be written as

1 f1

Ст — – crC/a I (Or2 — kr) dr.

2 ■ . Jo

Untwisted Blades, Uniform Inflow

For a blade with zero twist, В = constant = во. Also, for uniform inflow velocity, which is assumed in simple momentum theory, к = constant. Therefore, in this case the thrust coefficient is given by

To find the direct relationship between Ct and the blade pitch, we can use the relationship between Ct and к as is given by the simple momentum theory in Chapter 2 (i. e., A.,- = kh =

/7S 7nT mi _ .. _ jy _

f^T/ z )• A nereiore,

This equation must be solved iteratively to find Ct for a given value of Bo. Alternatively, solving directly for the pitch angle, Bq, in terms of an assumed thrust gives

The first term is the blade pitch required to produce thrust, and the second term is the additional pitch required to compensate for the inflow resulting from that thrust.

Figure 3.2 shows results for the thrust versus collective pitch for four rotors of different

сліігіїіл; г ГКо <avnarimflnto1 rlo+o оі*д tolzon fm-m fliA avnorlmonfc ni rrVif jfr Uafnor (1

OV/llUllj. JLUV VA^rVlUUWlUm UttlU CUV UUVV11 UVU1 111V VApVlllllVUtJ VI ivmgui LV X1VJLJL1VA r

who tested subscale rotors with no blade twist. These rotors involved increasing the number of blades to arrive at larger solidity, but there are no experiments that have examined solidity effects independently of blade number. The effect of number of blades (other than solidity) on the rotor aerodynamics, however, is small. For the purposes of these calculations, C/ff was set to a value of 5.73/radian, which represents a small reduction of the 2-D thin-airfoil result of 27r/radian because of finite airfoil thickness and Reynolds number effects. The agreement between Eq. 3.23 and the measurements is found to be good, although there is a slight overprediction of the thrust because so far the nonuniformity of the inflow and nonideal effects, such as tip loss, have not been accounted for in the theory.

5 10

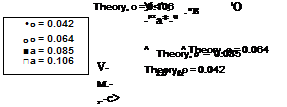Blade-pitch angle, 0О – deg.

Figure 3.2 Variation in rotor thrust coefficient with collective pitch for rotors with different solidities. Data source: Knight & Hefner (1937).