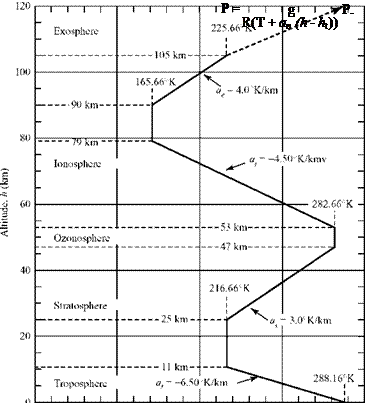
Atmospheric Property Variations in Gradient Layers

The thermodynamic properties for the various layers can be estimated by solving the appropriate equations. In a gradient layer, such as the troposphere, the tempera­ture is assumed to change linearly in such a way that:

is a constant. Therefore, by integration for a given gradient layer,

T(h) = T + a„(h – hi), (2.30)

where T is the temperature at some altitude h in the gradient layer, n (n = t, s,i, and e stand for troposphere, stratosphere, ionosphere, and so on). Then, from the ideal-gas

equation of state (Eq. 2.1), we can find a relationship among the pressure, altitude, and density:

This then can be inserted into Eq. 2.28 to replace the density so that only the pressure and altitude variables remain. Thus,

where the variables were separated. This simple differential equation can be solved easily by integration, with the result:

where C1 is the constant of integration. Rearranging,

can be evaluated by using known values of p and T at a given altitude. For example, in the troposphere, we can evaluate the constant of integration by using the fact that the sea-level pressure and temperature are pSL = 1.01325 x 105 N/m2 and TSL = 288.16°K. Then, with an = at = -6.5°K/km in the troposphere, and letting the reference point be at sea level (hi = 0, Ti = 288.16°K), the constant of integration is:

Ci = ps{Tsfg/anR).

Now, all the basic properties are available at any altitude in the troposphere gradient layer: Eq. 2.30 gives the temperature, Eq. 2.33 gives the pressure, and Eq. 2.31 gives the density.

Other properties such as the speed of sound and coefficient of viscosity that are mainly functions of temperature also can be determined. For example, the speed of sound, from Eq. 2.6, is:

a = -lyRT,

and using Sutherland’s Law, the viscosity coefficient is 3

2 T0 + S1 T + S :

where for air, S1 = 111°K, and —0 = 1.81 x 10-5 kg/m s and T0 = 273.2°K are reference values. The kinematic viscosity, v, often is needed. It is simply the ratio:

v = kinematic viscosity coefficient = — (2.35)

P

of quantities already known at a given altitude.

Notice that armed with these results, the atmospheric properties can be evalu­ated at any altitude within the layer and at the upper edge of the layer. The latter information then is used to evaluate conditions in the next layer.