COMPLEX REPRESENTATION OF HARMONIC MOTIONS

In the discussion of periodic phenomena, it is convenient to use the complex representation. Consider a quantity x which varies periodically with frequency m (radians per second) according to the rule:

x — A cos (tot + y>) (1)

This is a simple-harmonic motion. A is called the amplitude and y> the

* For aircraft structures, see Scanlan and Rosenbaum.1-67 For general principles, see Den Hartog,1-62 Timoshenko.1-69 Myklestad’s book1-66 treats the numerical aspects of the analysis.

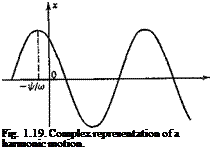
phase angle. It is customary to regard x as the projection of a rotating vector on the real axis (see Fig. 1.19). The length of the vector is A and its angle with the x axis is cot + f – The vector rotates counterclockwise with angular speed со. Since such a vector is specified by two com­ponents, it can be represented by a complex number. For example, the vector in Fig. 1.19 can be specified by the components a; = A cos (cot + ip), and у = A sin (cot + ip), and hence by the complex number x + iy. But

eH<at+y>) _ cos _}- y) _|_ / sin (+ ip) (2)

so the rotating vector can be represented by the complex number

x + iy = Aei(a, l+v) (3)

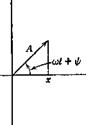The quantity x given by Eq. 1 is the real part of the quantity given by

Eq. 3, which is the complex representation of Eq. 1. The imaginary part of Eq. 3 represents another simple harmonic motion.

The vector representation is very convenient for “composing” several simple-harmonic oscillations of the same frequency. For example, if

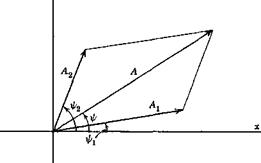
x = A1 cos (соїt + щ) + A2 cos (cot + ip2) — A cos (cot + ip) (4)

then x is the resultant of two vectors as shown in Fig. 1.20. The com­ponent A 2 cos (cot + f2) is said to lead the component Аг cos(cof + ірг), if, as shown in the figure, ip2 > Wi – Hereafter we shall write x given by Eq. 1 in the complex form

x = (a + іЬ)еш = Aei(",ti’l’) (5)

where

A = Va2 + b2, tan y> = –

a

It is understood that the physical quantity is given by the real part of the complex representation.

where, if /32 < 4Km*

Since the vector і leads the vector 1 by an angle tt/2, a multiplication of a given vector by the imaginary number і simply means a change of phase angle to lead by tt/2.

Fig. 1.20. Vector sum of two simple harmonic motions of the same frequency.

As an illustration, let us consider the forced oscillation of a single particle, with elastic restraint and with damping, excited by a simple – harmonic force. The equation of motion, written in real form, is

dhi dx

(6)

,Kx = Fa sin at

The solution may be written as

x = x1 + x2

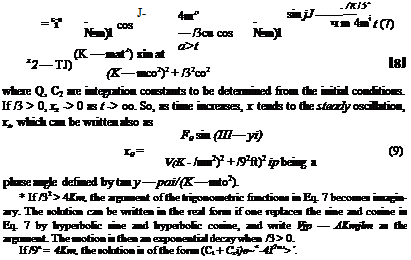These results can be derived by using the complex representation as follows. Consider the equation

md^ + Pjt+Kx = F^ (10)

Since F0emt = F0 cos ait + ifо sin cut, the real part of x will give the solution for a periodic force F0 cos cot, whereas the imaginary part that of F0 sin <ot. Putting x proportional to eiat, we obtain

dot

m— + (}—+Kx== {т{іт)г + /?/со + K]x (11)

Hence we obtain the steady oscillation

The modulus of Z(/co) is V(K — mw2)2 + /?2co2, and its phase angle is ip = tan”1 [fia)/(К — тш2)]. Since x is the ratio of two complex numbers, and since we divide two complex numbers by dividing their moduli and subtracting their arguments, we obtain

FJ(M-v)

x = (14)

V(K – ты2)2 + р2ш2