COUPLED TORSION-FLEXURE OSCILLATIONS OF A CANTILEVER BEAM

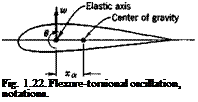We shall show that the oscillation of a beam whose elastic axis and line of centers of gravity do not coincide is always “coupled”; i. e., it is a combination of flexure and torsion. Let xa be the distance between the elastic axis and the line of center of gravity (Fig. 1.22). Assume that the elastic axis is a straight line and that the deflection of the elastic axis is

restrained to the vertical direction only. Let the vertical deflection be w and the rotation of the beam cross sections about the elastic axis be 6. Then the equations of motion are, according to Eqs. 5a and 6a of § 1.1,

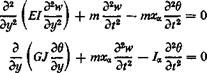0)

with the usual boundary conditions of a cantilever beam:

At	У = о,	W	-Ії-в-о ду
At	y — U	9 2и>	d3w Эб _ ~ эу3 эу
Зу2

These equations reduce to two independent ones for the purely torsional and purely flexural oscillations if xa = 0.

Again we look for particular solutions in the form

w(y, t) = A f(y)eM, 6(y, t) = B ф(у)еш (3)

Substituting Eq. 3 into Eq. 1, we obtain

with the corresponding boundary conditions obtained by replacing w by f and в by ф in Eqs. 2. Let us first remark that, by a generalization of the Sturm-Liouville’s theorem, it can be shown that there exist real valued eigenvalues to, and hence real-valued eigenfunctions f(y) and <f>(y). With­out proving this, we may verify it a posteriori by assuming that real to, f ф exist, and then carry through the computations to show that we can obtain them.

Let f(y) and ф(у) be solutions of Eqs. 4. Multiply the first and the second of Eqs. 4 by / and ф respectively, and integrate the results with respect to у from 0 to /. The following equations are obtained:

An integration by parts and an application of the boundary conditions (Eqs. 2) transform au and a22 into the following form:

«її – сиш1 ci2aj2 C210)2 «22 — C220j2 Pw* – Qu>2 + R = о

For a nontrivial solution, A and В must not both vanish. In order that a significant solution may exist, the determinant of the coefficients of Eqs. 5 must be zero:

It can be verified that the right-hand side of Eq. 11 is always positive. We obtain, therefore, four real roots for to. Hence, four particular

solutions are obtained, each representing a simple-harmonic motion. The ratio AIB, corresponding to each root w, is obtained from Eqs. 5:

A ^22^ #22

В cuw2 – #u c12co[5]

Thus, if f(y) and ф(у) were known, the constants #u, a12, etc., and P, Q, R can be computed according to Eqs. 6, 7,’10; and the frequency со and the ratio A/В can be obtained from Eqs. 11 and 12. To determine f(y) and ф(у), the method of successive approximation can be used. Let f0(y) and <f>Q(y) be two arbitrary functions which satisfy the “rigid” boun­dary conditions* at the clamped end у = 0, which are given by the first of Eqs. 2. Considering f0 and ф0 as approximate solutions, we determine the corresponding approximate values of #n, a12, ■ ■ ■ and со2 and A/B. Now, by a formal successive integration, Eqs. 4 may be written as

So the process of approximation can be carried out as follows: Substi­tuting /0 and ф0 into the integrands on the right-hand sides of Eqs. 13, we

obtain two new functions ~^Лу) and ф(у), which we shall call f(y)

and ф-fy). Using ffy), фх(у) as the first approximation, we determine au, #i2, etc., and со2 and A/В. If we substitute fv фг, and the new value of A/В into the integrands of Eqs. 13 and integrate, the result may be labeled /2 and ф2. The process can be repeated with f2 and ф2 as the starting approximations. When fn and фп converge satisfactorily, со2 and A/В must also converge to their true values. The rate of convergence depends on the choice of f0 and ф0. If /0 and ф0 were chosen as the fundamental modes of uncoupled flexural and torsional oscillations of a uniform beam, a sufficiently accurate result can usually be achieved in three or four cycles.

Let us assume that, in the process indicated above, we always take the smaller of the two to2 values of Eq. 11. It can be shown1-58 that, for

arbitrary choice of f0, ф0 (which satisfies the boundary conditions), the process of successive approximation converges to the fundamental mode of the coupled flexure-torsional oscillation, i. e., the mode with the lowest frequency.

If the larger of the two to2 values of Eq. 11 is taken in the successive approximation, a different set of values A/B, f(y) and ф(у) will be obtained, which would converge to the second mode of the flexure-torsional oscilla­tion. The physical meaning of the two modes can be clarified by the following illustration. Consider a beam whose center of gravity at each section lies exactly on the elastic axis (жа = 0). Such a beam can oscillate in purely flexural and purely torsional modes. If the center of gravity is moved away slightly from the elastic axis, the modes will change slightly, and the oscillation will be a combined flexure-torsional motion. With small values of жа, it is expected to have one of the combined flexural – torsional mode vary but little from the purely torsional mode, and the other vary but little from the purely flexural mode. Accordingly, one of the coupled oscillations is said to be predominantly flexural, and the other predominantly torsional.

It might appear that, if the center of gravity is moved further away, the frequencies may approach each other and finally coincide. Fora cantilever beam, however, this will never happen, because the frequencies can co­incide only if Q2 — APR = 0, and it can be verified that Q2 — APR is always positive if x* Ф 0. Hence, the roots must be discrete.

In order to obtain higher modes by the method of successive approxi­mation, the orthogonality relations among the normal modes may be used.1-52-1 05 But this subject will not be pursued further here.

The natural frequencies can be found experimentally by a resonance test. The oscillations may be excited, for example, by a rotating eccentric weight driven by a motor through a flexible shaft. Intense oscillations occur when the frequency of the motor coincides with one of the natural frequencies of the wing. As discussed above, the excited resonance oscillation is always coupled unless the elastic axis coincides with the inertia axis. But one of the modes will be predominantly flexural, and the other predominantly torsional. It is customary to call the first one flexural oscillation and the second one torsional oscillation.