Jump Conditions: Shock and Expansion Waves

The jump conditions associated with the system of first-order PDEs

I a – m?) du + dw =0

dw ди

dX — д = 0

where n = (nx, nz) is a unit vector normal to the jump line. Upon elimination of the normal vector, the shock polar is obtained:

(M? — 1) < и >? — < w >?=

— 1 < и > + < w >^ — 1 < и > — <w>^ = 0 (4.41)

The shock polar is made of two straight branches in the hodograph plane (< и >, < w >), J+:@ < и > + < w >= 0 and J—:в < и > — < w >= 0, see Fig.4.5. The origin of the hodograph plane corresponds to infinitely weak waves, i. e. characteristic lines, the half-plane < и >< 0 represents shock waves and the half-plane < и > 0 represents expansion waves.

The slope of the jump lines J+ and J— in the physical plane are obtained by selecting a root and using one of the jump relations

dz nx < и >

dx nz < w >

(dz) = 1 = (dz) , (dz) =—1 = (dz) (4.4?)

dx J+ p dx C+ dx J — p dx C—

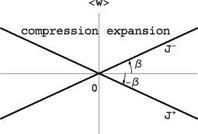Fig. 4.5 Shock polar for linearized supersonic flow

Fig. 4.6 Supersonic flow past a double wedge. S is a shock, E is an expansion “fan”

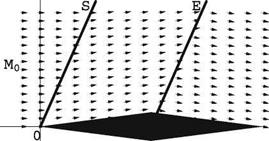Note that in linear theory the jump lines coincide with the C + and C – characteris­tics, Fig.4.4, and are perpendicular to their images J+ and J – in the hodograph plane, respectively. Shockwaves as well as expansion fans are represented by characteristics lines across which the velocity vector is discontinuous. Shocks can be differentiated from expansion waves by the fact that the u -component decreases (pressure increases) across them when following a particle, whereas the u-component increases (pressure decreases) as a particle crosses an expansion line. Figure4.6 depicts the flow past a double wedge profile at zero incidence. Note also, that in linear theory, an expansion fan collapses on a single characteristic line which acts as an “expansion shock.”