Linearized Compressible Flow Potential Equation

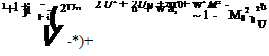As before, we will assume that the uniform flow is only slightly disturbed by a thin airfoil at incidence, where the incidence is also a small parameter, a ^ 1. The above density-velocity relation can be expanded for small values of u and w to read

The relative change in density is a more meaningful number and takes the form

which states that the Mach number is an amplification factor of the compressibility effects: the larger the Mach number, the larger the relative changes in density for a given longitudinal perturbation in velocity. Note that the incompressible limit is recovered for M0 = 0. The changes in density are considered negligible when M0 < 0.3. On the other hand, when M0 > 0.3, compressibility effects are expected.

The linearized Cp can also be derived from the density-velocity relation. Fist notice that the pressure ratio of local pressure to the undisturbed pressure is to first order

(4.8)

and using the identity ip0M^ = p0U2, simplifies the pressure coefficient to read, as before

in compressible, 2-D flow.

The tangency condition is also unaffected by the changes in density and remains

w(x, 0±) = U (f ‘±{х) – a) (4.10)

The equation of conservation of mass is nonlinear. The last step is to linearize it using the result just obtained for the density. The mass flux components are expanded as

p(U + u) = P0 (1 – M2U) U (1 + u) = poU (1 + (1 – M2)U + …) pw = P0U (w + )

(4.11)

where the second and higher order terms have been omitted. Substitution in the mass conservation yields a linear system of two first order PDEs

2 du dw M0 Ш + dz = 0	(4.12)
dw du dx dz 0	(4.13)

The irrotationality condition allows to introduce a velocity potential for the per­turbation velocity such that u = ^ and w = ддф. The conservation of mass is transformed into a second order PDE

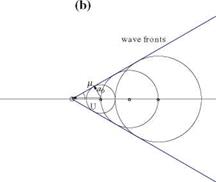called the subsonic linearized compressible flow potential equation when M0 < 1 and the potential equation for linearized supersonic flow when M0 > 1. The change of sign of the coefficient 1 – M0 is significant in associating different physical phenomena with different equation types, elliptic for subsonic flow with perturbation decay in all directions, and hyperbolic for supersonic flow with subdomains separated by wave fronts. This can be illustrated by a moving source emitting sound waves at equal intervals and examining the development of the wave fronts for Mach number aU < 1 and aU > 1, Fig.4.2. In subsonic flow, the waves move away from the source and the source influence is felt everywhere. The perturbations of the supersonic source are confined within a wedge (a cone in 3-D).

In supersonic flow, the wave fronts admit envelopes which make an angle j, called the Mach angle, with the flow direction. It is easy to see from Fig.4.2 that the Mach angle is given by

(4.15)