STEADY-STATE DESCRIBING FUNCTION

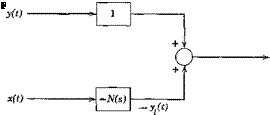
The relations implied by Fig. 3.22 can be reinterpreted as in Fig. 3.23. Now applying (3.4,50) we get the spectral density of r(t)

Фгг(ю) = Ф vv(a>) — Ж(іт)Фух(со) — 1У*(ісо)Фет(со) + N*(im)N(ia>№xx(co)

(3.5,2)

Since Фух = Ф*,, by (2.6,156), then

Ф„(со) = Ф„(а>) — [Фух{т)Щіт) + (Фда(со).Щі«))*] + N*{im)N(im) Фет(о)

(3.5,3)

We now wish to find the particular function N(im) that minimizes r2 — Фrr(co) dm. This can be done by the classical method of variational calculus, as follows.

Let us assume that N(im) is not exactly that which minimizes r2 but differs from it slightly, i. e.

N(im) = M(im) + ef(iw) (3.5,4)

where N(im) is the optimal function sought,/(ten) is an arbitrary continuous function, and e is a small parameter. Then N(im) is given by the solution of

– Рф„(со) dm =0 (3.5,5)

Эе J — GO €=0

When (3.5,4) is substituted into (3.5,3) and the l. h.s. of (3.5,5) is evaluated, the result is

f00 {-№,»/(»•<*>) + ф ;»/*(«>)]

J~ oo _ _

+ Ф«М[^*(мо)/(му) + f*(im)N(im)]}dm = 0 or

{І{іт)[Фхх(т)В*(іт) – Ф„»]

+ Г(іт)[Фхх(т)Щш) – Ф?»]} dm = 0 (3.5,6)

Since / (im) is an arbitrary function, the integral can only be zero if the two expressions in square brackets are both zero. Since one is simply the conjugate of the other they are simultaneously zero, and the required condition is

Щіт) = Щіт)