UNIQUENESS OF THE SOLUTION

The physical problem of finding the velocity field for the flow created, say, by the motion of an airfoil or wing has been reduced to the mathematical problem of solving Laplace’s equation for the velocity potential with suitable boundary conditions for the velocity on the body and at infinity. In a space-fixed reference frame, this mathematical problem is

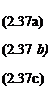У2Ф = 0

ЭФ к я

= n • qs on bod

УФ —» 0 at r —> °°

Since the body boundary condition is on the normal derivative of the potential and since the flow is in the region exterior to the body, the mathematical problem of Eqs. (2.37a, b, c) is called the Neumann exterior problem. In what follows we will answer the question “is there a unique solution to the Neumann exterior problem?” We will discover that the answer is different for a simply and multiply connected region.

Let us consider a simply connected region first. This will apply to the region outside of a three-dimensional body but care must be taken in extending the results to wings since the flowfield is not irrotational everywhere (wakes). Assume that there are two solutions Ф, and Ф2 to the mathematical problem posed in Eqs. (2.37a, b, c). Then the difference

Фі – Ф2 = Ф0

satisfies Laplace’s equation, the homogeneous version of Eq. (2.37b), and Eq. (2.37c).

One form of Green’s (George Green, German mathematician, early 1800’s) theorem (Ref. 1.5, p. 135) is obtained by applying the divergence theorem to the function Ф УФ where Ф is a solution of Laplace’s equation, R is the fluid region and S is its boundary. The result is

f Г ЭФ

J V<t>-V<PdV = J Ф — dS (2.38)

Now apply Eq. (2.38) to Ф0 for the region R between the body В and an arbitrary surface 2 surrounding В to get

f VФD • УФД dV = f Ф„^<« + f Ф0^5 (2.39)

Jr Jb Jz

If we let 2 go to infinity the integral over 2 vanishes and since Эф0/дп = 0 on В we are left with

f VФD^VФDdV = 0 (2.40)

Jr

Since the integrand is always greater than or equal to zero, it must be zero and consequently the difference Фі — Ф2 can at most be a constant. Therefore, the solution to the Neumann exterior problem in a simply connected r^»Vn ia unique to within a constant

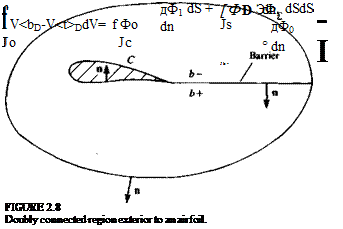
Consider now the doubly connected region exterior to the airfoil C in Fig. 2.8. Again let Ф! and Ф2 be solutions and take

Ф, Ф = Ф0

Green’s theorem is now applied to the function Фв in the region о between the airfoil C and the curve 2 surrounding it. Note that the integrals are still volume and surface integrals and that the integrands do not vary normal to the plane of motion.

Insert a barrier b joining C and 2 and denote the two sides of the barrier as b— and b+ as shown in the figure. Note that n is the outward normal to b— and — n is the outward normal to b+. Equation (2.38) then becomes

The integral around C is zero from the boundary condition and if we let 2 go to infinity the integral around 2 is zero also. Let Фр be Ф0 on b – and Фр be Ф0 on b+. Then Eq. (2.41) is

f УФР • УФ0 dV = | ФЪ^-dS – JT ФІ^dS (2.42)

The normal derivative of Фр is continuous across the barrier and Eq. (2.42) can be written in terms of an integral over the barrier:

f 7Ф* • dV = f (ФБ – Ф£) ^ dS (2.43)

Jo ^barrier

If we reintroduce the quantities Ф, and Ф2 and rearrange the integrand we get f УФ о • УФо dV=f (Ф Г – ФЇ + Ф2+ – Ф2~) ^ dS (2.44)

Ja ^barrier

Note that the circulations associated with flows 1 and 2 are given by

Г, = Ф^-ФГ

г2 = ф2+-ф2-
and are constant, and finally

f V<PD • V<&D dV = (T2 – Г0 f ^ ds (2.45)

*o -^barrier

Since in general we cannot require that the integral along the barrier be zero, the solution to the Neumann exterior problem is only uniquely determined to within a constant when Г, = Г2 (when the circulation is specified as part of the problem statement). This result can be generalized for multiply connected regions in a similar manner. The value of the circulation cannot be specified on purely mathematical grounds but will be determined later on the basis of physical considerations.