Applications of the Continuity Equation in Control-Volume Form

The integral form of the continuity equation is now applied in typical situations. Stu­dents should attempt to work through each example to check their understanding of the principles involved and then compare results to the detailed solutions. It is imperative that students develop a thorough understanding of the continuity result. Mathematical representations of flow fields that obey the continuity rules are said to be physically realizable flow patterns. We see later that it is possible to find solutions of certain problems that do not conform to reality because they are not continuous in the sense of satisfying continuity requirements.

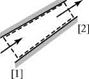
example 3.1 Given: Water flows steadily through a pipe at moderate pressure. The cross-sectional areas at Stations 1 and 2 are 2 m2, and 0.5 m2, respectively. The velocity at Station 1 is measured as 3 m/s. The flow is assumed to be one­dimensional; that is, variations in velocity across any cross-sectional area of the pipe are small compared with velocity variations along the length of the pipe. Thus, the velocity in the pipe at any cross-sectional area may be considered constant across the area.

Required: Predict the velocity at Station 2.

Approach: The flow is steady and a liquid is essentially incompressible. No details are needed between the two stations. Thus, apply the continuity Eq. 3.26.

Solution: First, the control surface, S, must be selected for this problem. Although any control surface may be chosen and gives the same answer, some thought usually suggests a choice that makes the calculation easiest. In this case, a cylindrical control surface (i. e., the dotted line) along the inner surface of the pipe with ends perpendicular to the flow velocities at the two ends is the best choice. Because there is no flow through the sides of the pipe, the integrand is zero everywhere except at the two ends. At the ends of the control volume,
the velocity and the unit outward normal are collinear so that (V • n) becomes simply the magnitude of the velocity, with signs positive for outflow and nega­tive for inflow. Thus,

j] (V • n) dS = JJ (V. n)dS + JJ (V ■ n)dS

s M Pi

= – V1 JJ dS + V2 J[ dS = – V1 A1 + V2 A2 = 0 [i] Pi

A (2)

So – "2=Vi A=3(0i=12m/s

Appraisal: The pipe area decreased from Station 1 to Station 2 and the velocity at Station 2 is found to be larger than at Station 1. This confirms experience from observations of water flow.

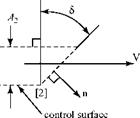The point was made in Example 3.1 that any control-surface choice leads to the same result. Suppose, for example, that the control surface at Station 2 was chosen so as to be at an angle 5 with respect to flow velocity at that point, as follows:

Then,

as before.

example 3.2 Given: A liquid (density 2.0 slugs/ft3) flows steadily through the pipe connection shown here. There is a mass flux into Station 1 with a magnitude гіг = 20 slugs/s. The mass flux out at Station 3 is гіг = 8 slugs/s. The flow through the pipe at the three stations may be assumed to be one-dimensional:

Required: Predict the volume flow and the flow direction (i. e., in or out?) at Station 2.

Approach: Choose a control volume that coincides with the inside surface of the pipe and is perpendicular to the inflow/outflow vectors at Stations 1, 2, and 3. Because the fluid is a liquid, assume incompressible flow. However, use Eq. 3.25 because the integrand corresponds to mass flux, which is the given for the problem even though the density, p, is constant. If the mass flux at Station 2 can be found, then the volume flow rate follows because the density is known. There must be three terms in the equation, corresponding to inflow or outflow at the three stations.

Solution: Using Eq. 3.25,

JJ p(V-n)dS = – mi+m3 ± m2 = 0,

S

where the signs at Stations 1 and 3 correspond to inflow (V. n < 0) and outflow (V . n > 0), respectively, and the sign of the term representing the mass flux at Station 2 is, for the moment, unknown. Substituting

-20 + 8 ± hi 2 = 0,

it follows that hi 2 must be positive, so that the flow at Station 2 must be outward and hi 2 = 12. Now, hi 2 = 12 = pVA = 2.0 VA, where A is the area of the pipe at Station 2. Solving, VA = volume flow rate = 6 ft3/s.

Appraisal: The physical fact is that for this steady flow, the mass flux into the connector must equal the mass flux out; there is no change in the mass of liquid within the connector. Because the density is constant, this states further that the volume flow rate out must be equal to the volume flow rate coming in.