DEFINITION OF THE ANGLES

THE VEHICLE EULER ANGLES

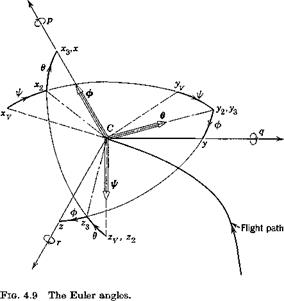
The orientation of any reference frame relative to another can be given by three angles, which are the consecutive rotations about the axes z, y, x in that order that carry one frame into coincidence with the other. This is a particular case of Euler angles. In flight dynamics, the Euler angles used are those which rotate the vehicle-carried vertical frame Fr into coincidence with the relevant axis system. Only two sets are commonly used, those for the body axes FB, and for the wind axes Fw. The angles are denoted (y>, в, ф) for body axes, including the special case Fs, and (ipw, 6W, фцг) for wind axes. Figure 4.9 shows the sequence of rotations.

(i) A rotation ф about OyZy, carrying the axes to Ovx^y2z2. гр is the azimuth angle

(ii) A rotation ® about Oyy2, carrying the axes to Ovx$3zs. в is the elevation angle

(iii) A rotation ф about 0vx3, carrying the axes to their final position Oyxyz. ф is the bank angle.

In order to avoid ambiguities which can otherwise result in the set of angles (y>, в, ф) the ranges are limited to

— 7Г < ip < TT or 0 < y> < 2tt

— – <:в <­2 2

— tr <, ф <. rr or 0 < ф < 2n

The Euler angles are then unique for most orientations of the vehicle, f although it should be noted that in a continuous steady rotation, such as rolling, the time variation of ф for example is a discontinuous sawtooth function.

As shown in Fig. 4.7, the angle 0lv is also commonly denoted by y, called the angle of climb for an obvious reason.

t There is an ambiguity for the angles defining a vertical dive, since (у, в, ф) = (a + b, —7t/2, —a) gives the same final orientation regardless of a. a = 0 would he the natural choice, and this special case does not seem to cause any difficulties.