Dynamics of Blade Flapping with a Hinge Offset

The analysis of a blade with a hinge offset is similar to the foregoing, but there are some important quantifiable differences. The blade is assumed to be rigid and hinged at a distance eR from the rotational axis. The forces acting on an element of the blade are as follows:

1. Inertia force m(y — eR)0dy acting at a distance (y — eR) from the hinge.

2. Centrifugal force myQ,2 dy acting at a distance (y — eR)0 from the hinge.

3. Aerodynamic lift forces L dy acting at a distance (y — eR) from the hinge.

Taking moments about the flapping hinge gives the equation of motion

In this case, the mass moment of inertia about the flapping hinge is

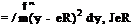
h

so that the flaDDine eauation becomes

[.. 0( eR fRm{y — eR)dy ) CR

/*|l + fl2(l + " eR h——————— —Jfi = J L(y — eR)dy. (4.63)

Dividing through by Q2 gives

h(*P 4- v2pp = ^ J L(y – eR)dy,

where vp is the nondimensional flapping frequency in terms of the rotational speed, that is,

fR

eR I m(y — eR)dy

= 1 + JeR,————————- . (4.65)

lb

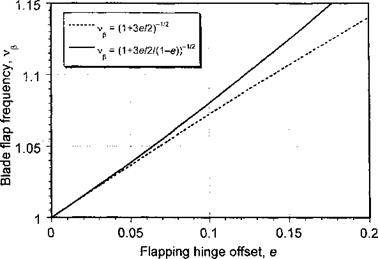
Again, the physical analogy with a spring-mass-damper system can be drawn. Eval­uation of Eq. 4.65 shows that the undamped natural frequency of the uniform system is now

the proof of which is the basis for Question 4.1. The behavior is shown in Fig. 4.9. Typically, the value of e varies from 4 to 6% for an articulated blade (although higher for hingeless

Figure 4.9 The blade flapping frequency varies with the hinge offset.

or semi-rigid rotors), so that the natural frequency of the rotor is only slightly greater than £2 or 1/rev. This also means that the phase lag between the forcing and the rotor flapping response must be less than 90° and the flapping displacements also now depend on aerodynamic damping. In this case, the flapping equation is

? + = УЩ, (4.67)

where vp is the rotating flapping frequency in terms of rotational speed. (Remember that vp = 1 for a hinge at the rotational axis.) Therefore, in hover the flapping response to cyclic pitch inputs is given by

А«(^-1) + Аа| = |е1с. (4.68)

Pu(v2f-l)-fiicj = jeu – (4.69)

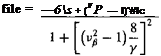This gives for the longitudinal flapping angle

and for the lateral flapping angle

In this case, the forcing frequency (1/rev) is less than the natural flapping frequency (off resonance condition) and it can be shown that the phase lag, ф, will be less than 90° as given by

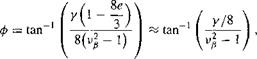(4.72)

which is a result considered in Question 4.7. For hingeless rotors, which have a relatively

high hi nap offset thp. пЬяяр. Іяа is flhnnt 7S—80°

О О ‘ — о ” ■’ ‘ ~ ‘ “ ’