GENERAL CONSIDERATIONS IN AERODYNAMICS AND THE DIMENSIONLESS COEFFICIENTS

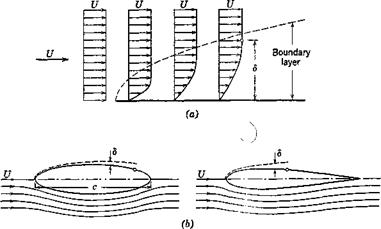
In order to discuss aeroelastic oscillations associated with the shedding of vortices, it is necessary to consider the effect of the viscosity of the fluid. In the flow of a nonviscous fluid the possibility of slip between the fluid and a solid body in contact with the fluid may be assumed. But such a relative velocity is impossible in a viscous fluid: The velocity of the fluid in contact with the solid must be exactly the same as that of the solid itself. This nonslip condition persists, no matter how small the viscosity of the fluit^fas long as the characteristic length of the body is much larger than the mean free path of the fluid molecules. But, when the viscosity is small, its effect is felt only in a thin layer next to the solid body: the boundary layer, in which the velocity of flow changes rapidly from the velocity of solid surface to that of the free stream. Outside the boundary layer, the fluid may be regarded as nonviscous, (see Fig. 2.2 in which the scale normal to the solid wall is greatly exaggerated).*

* The boundary layer thickness <5 in Fig. 2.2 is defined by the condition that, when the distance from the solid wall is (5, the retardation of the velocity of flow due to the skin friction is 1 per cent of the potential flow velocity; i. e., at S, the velocity attains 0.99 of the potential value. For a given body, the boundary-layer thickness decreases as the Reynolds number increases. At higher Reynolds number, the flow in the boundary layer is laminar near the leading edge, but becomes turbulent behind a transition point. As shown in Fig. 2.2c, the transition point moves forward as the Reynolds number increases. A turbulent boundary layer can resist an adverse pressure gradient better than a laminar one, and separation over an airfoil can be delayed.

The flow in the boundary layer is pulled forward by the free stream, but is retarded by friction at the solid wall. It is also retarded by an adverse pressure gradient, if such a gradient exists. If the adverse pressure gradient is sufficiently large, the flow may be interrupted entirely, and the

boundary layer may detach from the solid wall. The flow is then said to be separated.

An adverse pressure gradient exists in a flow around a bluff body, such as a cylinder or a sphere. For a streamlined body, such as an airfoil, the rear part of the body is very thin and has very gentle curvature; the adverse pressure gradient is small, and separation can be prevented. A streamlined body maintains a smooth flow when it is properly situated in
the flow; but, when the angle between the chord and the undisturbed stream is sufficiently large, separation may still occur.

The above physical picture explains why the Reynolds number is so important in determining the condition of flow around a bluff body and the force acting on it, because the Reynolds number expresses a ratio between the inertia force and the friction force. A flow pattern is deter­mined by the interplay among the pressure gradient, friction, and inertia. As these three forces are subject to the condition of equilibrium, only two of them are independent, and we may select the friction and inertia as independent influences. The inertia force has components of the form

and, hence, for a given flow pattern, must be proportional to the products pU2jl, where U is a characteristic velocity, and / a characteristic length. On the other hand, the friction force has components of the form у(д2и/ду2), and, hence, for a given flow pattern, must be proportional to yU/l2. (Э2m means a small difference of velocity of the second order, and is therefore proportional to the velocity U, whereas Эy2 is the square of a small difference in length and is proportional to /2.) The ratio between these two forces is therefore

PU2 . yU pUl
І ~ l2 ~ у

which is the Reynolds number.* A small value of Reynolds number means that friction forces predominate; a large value that inertia forces predominate.