Inviscid, Unsteady Flows Past Airfoils

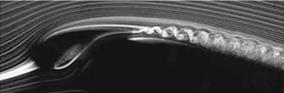
In this chapter we will study 2-D unsteady incompressible flows such as flow past oscillating profiles or impulsively accelerated airfoils. The flow is assumed to be uni­form and potential in the far field. In such cases, the profile contains time dependent bound vorticity and the wake contains shed vorticity that is convected downstream and influences the profile flow conditions. An example of wake shedding vorticity is shown in Fig. 5.1. Unsteady compressible flows are also covered.

5.1 Unsteady Incompressible Flows

5.1.1 Unsteady Flow Past Thin Cambered Plates: Governing Equations

This section is the extension of thin airfoil theory to unsteady flow. Thickness is not considered here as it does not contribute to forces and moment. Consider a uniform incoming flow of velocity U parallel to the x-axis. The total velocity is V = (U + u, w), where (u, w) represent the perturbation velocity components. The governing equations are still conservation of mass and irrotationality for the perturbation velocity

Fig. 5.1 Vortex shedding from a slat trailing edge (courtesy M. Asai, Fluid Dynamics Laboratory, Tokyo Metropolitan University)

© Springer Science+Business Media Dordrecht 2015

J. J. Chattot and M. M. Hafez, Theoretical and Applied Aerodynamics,

DOI 10.1007/978-94-017-9825-9_5

Note that this system is identical to that at steady-state. This is because we assume incompressible potential flow = 0). The unsteady effects will appear through the boundary conditions. Lets assume that the cambered plate can rotate by a small angle a(t) about an axis located at xQ along the x-axis and can translate parallel to the z-axis with a small amplitude h (t). The equation of the thin cambered plate at time t is given by

z±(x, t) = d(x) + (xq — x)a(t) + h(t) (5.2)

The tangency condition reads

(v’r – П = 0

profile

where V r = V — V e is the velocity of the fluid in a frame attached to the profile (relative velocity) and V e is the entrainment velocity due to the motion of the profile. The entrainment velocity for a point on the profile is given to first order by

d a dh

V‘ = (°-(xq —x)d + si) (5-4)

Hence the relative velocity is

d a dh

Vr = U + u, w — (xq — x) — (5.5)

dt dt

A unit normal vector to the profile is to first order it = (d'(x) — a(t), —1).

The tangency condition can be simplified by keeping the first order contributions only and, as was done in steady flow, by transferring the condition to the x-axis between 0 and c as

Such a flow can be modeled by a distribution of bound vorticity Г'(x, t) along the chord [0, c] representing the vorticity inside the profile (bound vorticity) as well as shed vorticity along the x-axis, x > c. The equation governing the shed vorticity is the linear convection equation for the circulation

дГ д Г

Ж + U dx = 0

The solution is made unique by requiring the Kutta-Joukowski condition to hold at the trailing edge, i. e.

(c, t) = 0 (5.8)

d x

In the far field the perturbation velocity decays, except near the x-axis, when shed vorticity is present

u, w ^ 0, x2 + z2 ^ro, almost every where (5.9)

The linearization of the mathematical model will be complete with that of the Bernoulli equation. For unsteady, potential flow, Bernoulli equation reads

дф V2 U2

p~rn + p + PT = pro + p T

Expanding the velocity term with the small disturbance assumption yields

дф

P + p + pUu = pro at

To first order, pressure is given by