Moving Sources
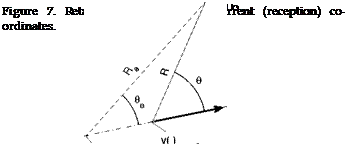
Retarded-potential formula, eq. (8) is a description in terms of stationary sources. In order to address separately features related to source physics and source motion, going back to eq. (7) and specifying the motion in the source distribution S is more appropriate. In this section, we consider an elementary point source of strength q moving at constant speed U0 = |Uo| in rectilinear motion (Fig. 7). Then S(y, t’) = —q(t’) S(y — U0t’). Performing first the volume integral and then the time integral, and using properties of the delta-function (Jones (1972)) yields the simple expression
where the index e refers to quantities evaluated at the emission time and where M0 = U0/c0 is the Mach number. Indeed in a moving-source context the source continues its motion along its path during the propagation towards the observer. The received information at (x, t) is naturally expressed as a function, not only of the source strength at the corresponding emission time but also of the retarded location ye = U0te, different from the current location y = U0t. The summation means that more than one retarded position is able to provide a contribution at (x, t) depending on the value of the Mach number. Using eq. (9) requires passage formulas between both sets of current and retarded coordinates. This is achieved by solving the retarded-time equation t’ = te(t) or equivalently by geometrical considerations on the sketch of Fig. 7. The result is
Rty = в (M0 cos e(t) ± /M° cos2 в(і) + в2) , (10)
cos ee(t) = M0 + R(jl cos 0(t) , (11)
Re (t)
with fi = J1 — M2.
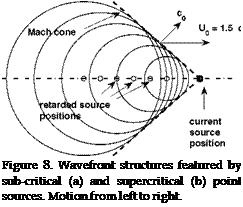
Equations (9) to (11) imply key features of the radiation process. First the Doppler factor 1 — M0 cos 9e in the denominator of eq.(9) causes anisotropy in the field, referred to as convective amplification. This is clearly understood from the instantaneous pattern of wavefronts emitted by the source at successive time steps, shown in Fig.8. For sub-critical motion (M0 < 1) all wavefronts get closer to each other in front of the source and spread away from each other behind. The quantity delivered by the source in the forward (resp. rearward) direction distributes in a smaller
 |
(resp. larger) volume between adjacent wavefronts, with respect to the case of a stationary source. The injection per unit volume is increased (resp. decreased), precisely in the ratio 1 — M0 cos ве.
Secondly, since Re(t) must be real and positive, the retarded-time equation always has a single root given by the sign + in the formula when M0 < 1, and has zero or two roots depending on the angle в for the supercritical regime M0 > 1 because both signs are acceptable. In this case the series of wavefronts intersect each other with a conical envelope called the Mach cone (Fig.8-b). As long as the observer is external to the Mach cone he cannot receive any signal, whereas once inside he always receives two signals from two different retarded locations.
Finally, if the source function is assumed monochromatic with strength q(t’) = q0 в-гШе l, the received signal cannot be monochromatic anymore. However performing a Taylor expansion of the solution around a reference time within a characteristic period of oscillation would restore an instantaneous frequency at observer ш = ше/(1—M0 cos ве). The received frequency is higher (resp. lower) than the emitted frequency for an approaching (resp. retreating) source. This frequency shift is known as Doppler effect. Again it is understood from Fig.8: an observer located in front of (resp. behind) the source receives wavefronts at a frequency higher (resp. lower) than the frequency emitted by the source, in the ratio of the Doppler factor.
For supercritical moving sources this factor has a singularity for the crit-
(a)
 |
 |
(b)
ical angle 0e = sin-1(1/Mo) encountered when the observer is exactly on the Mach cone attached to the source, at which the formalism breaks down. In order to give sense to the singularity, the supercritical moving elementary source can be simulated thanks to the identity with a linear distribution of stationary phased sources, provided that finite time and space scales are associated to the sources. This is illustrated in Fig. 9 in a discretized form with a series of impulses emitted by a linear array of sources, similarly to
Figure 9. Formation of a focused wave on the Mach cone of a supercritical source, synthesized by 17 Gaussian spots. Simulated Mach number M0 = 2, motion from left to right. From (a) to (d), successive time steps, gray scale updated for clarity.
what happens with Christmas electric garlands. Gaussian impulses which are solutions of the wave equation in spherical coordinates are used, according to the wave pattern y>(r, t) = [(r — c0 t)/r] e – a (r-c° t’) , where a is a parameter. Seventeen stationary sources are taken in the example to simulate a motion at Mach number 2 and the waves are superimposed at different time steps to produce the plots of the figure. The signal is found to focus as a spot on the Mach cone whereas it is rapidly attenuated in other directions. A closer look at the solution would exhibit a decay like the inverse square root of the propagation distance in the direction normal to the cone. Therefore the Doppler singularity is interpreted as a focused cylindrical wave in three-dimensional space (see Ffowcs Williams (1993)). When this happens with acoustic sources, sound propagates at much larger
distances than what is expected from simple spherical spreading. In aeroa- coustics, such focused waves are encountered in supersonic jets because of supersonically convected quadrupoles. The mechanism is known as ’Mach – wave radiation’. Advancing blade tips of high-speed helicopter rotors also produce equivalent waves because of quadrupole sources onset within the air beyond the tip radius and moving supersonically.
It is worth noting that for a supersonically flying aircraft, the Mach cone of the acoustic sources is hidden by the shock wave structure attached to the aircraft. The shock wave is a non-linear, compressible aerodynamic feature, whereas the Mach cone is a linear wave envelope, but the both of them have the same angle.
All preceding features refer to the wave equation and can be observed as well in particle physics and in water waves. For instance the formation of a Mach cone for supercritical particles in the high atmosphere is known as the Cerenkov effect, and a similar pattern is generated when making ducks and drakes on water surface with a flat stone. Further aspects of source motion in aeroacoustics accounting for space and time correlation scales are discussed by Crighton (1975).











