Supersonic Flow Adjacent to Uniform Flow Region

We consider the subdomain SW delimited by the C+ which bounds the uniform flow region where the perturbation velocity is (u1, 0) and the C— characteristic through the point of intersection of the former with the Ox-axis, Fig. 4.21.

Plane Flow

In the case of plane, near sonic flow (M0 = 1), the compatibility relations given earlier are

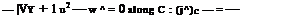
1

(Y+1)u

(4.136)

We consider the change of independent variables from (x, z) to (£, Z) where £ = const along C + characteristics and Z = const along C— characteristics. One such transformation is given by

d £ — dx — /(y + 1)udz — dx + didz

/______ dZ (4.137)

d Z = dx + V (y + 1)udz = dxdx + f^dz

Let u(x, z) = U(£, Z) and w(x, z) = W(£, Z). Using the chain rule, the total derivative along the C + characteristic can be written

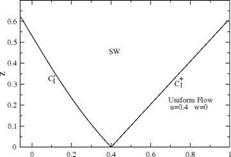Fig. 4.21 Subdomain SW adjacent to uniform flow region

The CR+ now reads

This PDE can be integrated to give

2 3

– 3>/7+Тu3 + w = /(Z), Vz, Zin sw

where / is an arbitrary function of a single argument. Similarly, with CR one finds 2 3

Y + 1U2 + W = h(Z), V Z, Z in SW (4.141)

This last relation can be fully resolved by taking into account that all C – charac­teristics in SW emanate from the uniform flow region, therefore [2]

Axisymmetric Flow

The compatibility relations now read

2 / 3 — ~2 y + 1u2 + w — 2 —y + 1u 2 —

CR+ ■ A. CR ‘ dx

C+

CR-: d

C-

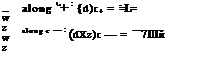(4.145)

We will use the same change of independent variables and verify that a simple wave solution exists in SW by assuming that u(x, z) = U(Z), V Z, Z in SW. The C R+ now reads

2 3 -jVT+l U [3] [4] + W

d W d w

= 2 = [w]c+ =——–

dZ dx z

This relation holds on a C + characteristic of equation Z = x — zV (Y + 1)U (Z) = const, hence one can write

d w dx

= — (Y + 1)U (Z) (4.147)

w x — Z

Upon integration one obtains ln |w| = —(t + 1)U(Z) ln |x — ZI + f (Z), where f is an arbitrary function of a single argument. Lets define the C— character­istic with parametric representation (xi(Z), zi(Z)) and characteristic Cauchy data (U(Z), W1(Z)) on C—. One finds

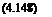/zi(Z) (Y+1)U (Z)

W(Z, z) = W1(Z) ^ , along C+

-3 yytt u (Z)2 — W1(Z^

d dx

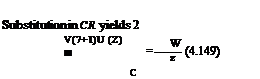The left-hand-side term can be expanded as

2 3 —3^гП и (Z)3 — w (Z, z)

d dZ

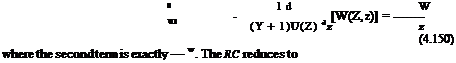
which, upon integration, yields

– 3VYГГU(03 – W1 (0 ^ = h(Z) (4.152)

along the C – characteristic. Note that along a C-, z is only a function of £, not of Z. Making use of the fact that the C – originate in the uniform flow region, one concludes that h(() = const., and the relation becomes

2 3 3 z,(n Тїт+ЇЖО

дл/т+ї u 12 – U(03 – wm ^ = 0 (4.153)

Along the C – , the characteristic initial data cannot be chosen arbitrarily since

|Vy + 1 ( u2 – U(02 ) – Wi(0 = 0 there. This completes the verification that

a simple wave solution exists in the SW subdomain. Although w(x, z) varies along C + characteristics, u(x, z) = U(£) is constant on a C+, implying that they are straight lines of slope. In this axisymmetric transonic small disturbance

approximation, a region adjacent to a uniform flow region is also a simple wave region.