The momentum equation
The momentum equation for two – or three-dimensional flow embodies the application of Newton’s second law of motion (mass times acceleration = force, or rate of change of momentum = force) to an infinitesimal control volume in a fluid flow (see Fig. 2.8). It takes the form of a set of partial differential equations. Physically it states that the rate of increase in momentum within the control volume plus the net rate at which momentum flows out of the control volume equals the force acting on the fluid within the control volume.
There are two distinct classes of force that act on the fluid particles within the control volume.
(i) Body forces. Act on all the fluid within the control volume. Here the only body force of interest is the force of gravity or weight of the fluid.
(ii) Surface forces. These only act on the control surface; their effect on the fluid inside the control volume cancels out. They are always expressed in terms of stress (force per unit area). Two main types of surface force are involved namely.
(a) Pressure force. Pressure, p, is a stress that always acts perpendicular to the control surface and in the opposite direction to the unit normal (see Fig. 1.3). In other words it always tends to compress the fluid in the control volume. Although p can vary from point to point in the flow field it is invariant with direction at a particular point (in other words irrespective of the orientation of the infinitesimal control volume the
pressure force on any face will be —p6A where 6A is the area of the face) – see Fig. 1.3. As is evident from Bernoulli’s Eqn (2.16), the pressure depends on the flow speed.
(b) Viscous forces. In general the viscous force acts at an angle to any particular face of the infinitesimal control volume, so in general it will have two components in two-dimensional flow (three for three-dimensional flow) acting on each face (one due to a direct stress acting perpendicularly to the face and one shear stress (two for three-dimensional flow) acting tangentially to the face. As an example let us consider the stresses acting on two faces of a square infinitesimal control volume (Fig. 2.20). For the top face the unit normal would be j (unit vector in the у direction) and the unit tangential vector would be і (the unit vector in the x direction). In this case, then, the viscous force acting on this face and the side face would be given by
+ <Tyyj)6x X 1, {oxxl + СГхуІ)6у X 1
respectively. Note that, as in Section 2.4, we are assuming unit length in the z direction. The viscous shear stress is what is termed a second-order tensor – i. e. it is a quantity that is characterized by a magnitude and two directions (c. f. a vector or first-order tensor that is characterized by a magnitude and one direction). The stress tensor can be expressed in terms of four components (9 for three-dimensional flow) in matrix form as:
|
( |
&XX &xy Gyx ®yy
Owing to symmetry axy = oyx. Just as the components of a vector change when the coordinate system is changed, so do the components of the stress tensor. In many engineering applications the direct viscous stresses (axx, oyy) are negligible compared with the shear stresses. The viscous stress is generated by fluid motion and cannot exist in a still fluid.
Other surface forces, e. g. surface tension, can be important in some engineering applications.
When the momentum equation is applied to an infinitesimal control volume (c. v.), it can be written in the form:
Rate of increase of momentum within the c. v.
‘————————- v———————– ‘
(i)
+ Net rate at which momentum leaves the c. v..
(И)
![]() = Body force + pressure force + viscous force
= Body force + pressure force + viscous force
V ^ s ^/ 41 s/ ^
(in) (iv) M
We will consider now the evaluation of each of terms (i) to (v) in turn for the case of two-dimensional incompressible flow.
Term (i) is dealt with in a similar way to Eqn (2.43), once it is recalled that momentum is (mass) x (velocity), so Term (i) is given by
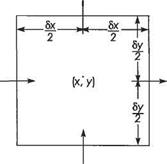
To evaluate Term (ii) we will make use of Fig. 2.21 (c. f. Fig. 2.12). Note that the rate at which momentum crosses any face of the control volume is (rate at which mass crosses the face) x velocity. So if we denote the rate at which mass crosses a face by m, Term (ii) is given by
![]() m3 x v3 – m, x у, + m4 x v4 – m2 x v2
m3 x v3 – m, x у, + m4 x v4 – m2 x v2
But m3 and m are given by Eqns (2.38) and (2.39) respectively, and m2 and m4 by similar expressions. In a similar way it can be seen that, recalling v = (и, v)
|
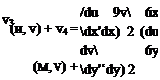 |
|
|
||
|
||
|
||
|
||
So the x component of Eqn (2.61) becomes
|
( du Sx ( du 6x ( du 8x ( dui 4"+stJ** 4"+&tJ“Т’аїХР* T-a-xi; f du6y dy 2 ) Hr dy 2 )X M dy 2 ) |
du 8x
![]() dv 6y dy 2
dv 6y dy 2
Cancelling like terms and neglecting higher-order terms simplifies this expression to
( du du dv
p[2ua-x + %+“^)lxSyx’
This can be rearranged as
![]()
![]() f du du (du 9v)
f du du (du 9v)
/,[иГх + %+и^+а~И )SxSy x
= 0 Eqn (2.46)
In an exactly similar way the у component of Eqn (2.61) can be shown to be
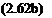 ( dv dv l’{ua-x+”Ty)6xlyxl
( dv dv l’{ua-x+”Ty)6xlyxl
Term (iii) the body force, acting on the control volume, is simply given by the weight of the fluid, i. e. the mass of the fluid multiplied by the acceleration (vector) due to gravity. Thus
![]() (2.63)
(2.63)
Normally, of course, gravity acts vertically downwards, so gx = 0 and gy = —g.
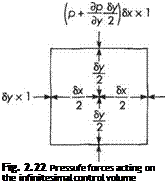
The evaluation of Term (iv), the net pressure force acting on the control volume is illustrated in Fig. 2.22. In the x direction the net pressure force is given by
|
‘-If,**1 |
6y x 1 = —^-SxSy x 1 (2.64a)
 ‘~lf)
‘~lf)
(-fib*1
Similarly, the у component of the net pressure force is given by
![]()
![]() dp,
dp,
dy
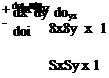 |
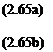 |
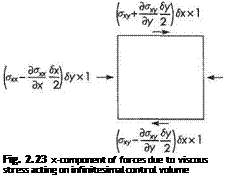
The evaluation of the x component of Term (v), the net viscous force, is illustrated in Fig. 2.23. In a similar way as for Eqn (2.64a, b), we obtain the net viscous force in the x and у directions respectively as
|
du du р{ді+иа-*+%. |
 |
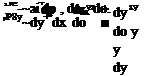 |
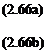 |
We now substitute Eqns (2.61) to (2.65) into Eqn (2.59) and cancel the common factor 8x8y x 1 to obtain
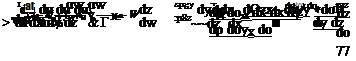 |
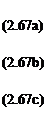 |
These are the momentum equations in the form of partial differential equations. For three dimensional flows the momentum equations can be written in the form:
where gx, gy, gz are the components of the acceleration g due to gravity, the body force per unit volume being given by pg.
The only approximation made to derive Eqns (2.66) and (2.67) is the continuum model, i. e. we ignore the fact that matter consists of myriad molecules and treat it as continuous. Although we have made use of the incompressible form of the continuity
 бух 1
бух 1
Eqn (2.46) to simplify Eqn (2.58a, b), Eqns (2.62) and (2.63) apply equally well to compressible flow. In order to show this to be true, it is necessary to allow density to vary in the derivation of Term (i) and to simplify it using the compressible form of the continuity Eqn (2.45).











