The Reynolds’ Transport Theorem

Examine each physical law described in Section 3.3. Notice that each law involves an extensive and a related intensive property of the fluid. For example, in Eq. 3.9, the extensive property E (i. e., the total energy of the entire system) is given by the integral over the system volume in which the differential element of energy is e’pd V (i. e., e’ the intensive variable, energy per unit mass, multiplied by a differential mass element pd V). Table 3.1 shows each extensive variable involved in the rate equations and the related intensive variable. One of the intensive variables is a constant, 1, because the differential mass element is 1 pd V.

Two of the variables are scalars (e’ and s) and two are vectors (V and r x V). What is needed is a way to represent the rate of change of each extensive variable as a volume integral (we also need surface integrals) over a fixed control volume instead of the moving system volume. Actually, it is not necessary that the control volume be fixed, but the analytical method is demonstrated here for the simplest case of a control volume fixed in space, as shown in Fig. 3.2.

The region illustrated in Fig. 3.2 is filled with a fluid moving relative to the con­trol volume (dashed outline). There is no restriction on the size, shape, or location in the flow field of the control volume. How these geometrical features are chosen to analyze a given problem is shown by example later in this chapter. For now, we choose the control volume so that at some arbitrary initial time, t, it coincides with our moving system glob, as illustrated in Fig. 3.2(a) with a solid outline. At a later

Table 3.1. Extensive and intensive variables Property Extensive Variable Associated Intensive Variable Mass m 1 Momentum p v Angular momentum h r x V Energy E e’ Entropy s s

instant of time t + At—for example,—the system has moved with the stream to a new location slightly displaced from the original one in Fig. 3.2(b). From the standpoint of the control volume, depicted by the dashed boundary, some of the system mass and its associated properties including momentum and energy flowed out through the surface, and new material similarly passed in to take the place of the part that

moved downstream. Notice that because a small but finite time is required for this to happen, it may be that there are corresponding small changes in both the physical properties of the fluid and in the direction and speed of the flow. We use the small­ness of these changes in the limit of a small time change, At ^ 0, to simplify the analysis. The result shows how to replace the time derivative of the system extensive variable into an equivalent control-volume representation.

What we show is that the rate of change of any intensive property can be written as the sum of the time rate of change of the volume integral over the control volume and a surface integral over the surface bounding the control volume. The latter accounts for the fact that the rate of change is due in part to the passage of mass and the associated physical properties through the surface of the control volume, as previously described.

The derivation is simply an extension of the ideas of differential calculus. It is useful to carry out the analysis for a representative property—for example, the energy—and then to generalize the final result for use with any other property. The energy balance is a good sample property because most students have worked extensively with it in basic thermodynamics courses. To use the First Law of Thermo­dynamics (Eq. 3.8), it is necessary to evaluate dE/dt for the system and then convert it into control-volume form. From the definition of the derivative:

dE

— = lim

dt At^Q

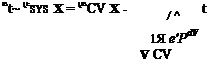where Et is the energy of the system of fluid particles at the initial time, t, and Et+At is the system energy at t + At, a short time later. At the initial time, the energy contained in the control volume is equal to that in the system because they occupy exactly the same space. For the moment, we append subscripts to distinguish between the con­trol volume (CV) and the system (SYS).Thus, at the initial time:

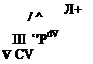At t + At, we must account for the fact that the system is displaced from the control volume, as illustrated in Figure 3.2(b). Thus, the integral:

is not equal to the system energy at the later time. To determine the system energy, Et+At, for use in the limiting process in Eq. 3.14, we must correct the control – volume integral (Eq. 3.16) in two ways. We must account for new energy that has passed into the control volume with the flow to make up for the void left by the system. This energy then must be subtracted from the energy given by Eq. 3.16. We also must add the energy in the part of the system that already has left the region of the control volume (i. e., that part of the system shown in Figure 3.2(b) to the right of the dashed boundary of the control volume), properly updated to the later time.

The two corrections can be handled simultaneously and simply by working with a differential volume such as that illustrated in Figure 3.2(b). Consider a dif­ferential surface element, dS, at any point on the surface of the control volume at time t (see Figure 3.2[a]). The outward pointing unit vector, n, is perpendicular to the control surface at that point. Notice that the velocity vector V at that point in the flow may be in any direction at an angle (e. g., 0) to the normal direction. Note, however, that at locations on the control surface where 0 < 90°, the flow is out of the control volume and that at locations where 0 > 90°, the flow is into the control volume. When 0 = 90°, there is no flow across the boundary because the stream­lines are then parallel to it. At the later time shown in Fig. 3.2(b), the part of the system bounded by the surface element dS moved with the flow to a new location at distance:

At = jvjAt = VAt

downstream. It is easy to see that in the limit of At ^ 0, the surface element sweeps out a volume:

АУ = cos 0 dSA£ = dS AL = n -VAt dS, (3.18)

where cos0 dS is the cross-sectional area of the stream tube and cos 0 is equal to the dot product between the normal n and the unit vector parallel to the local velocity vector (V/V). The mass contained in that volume element is equal to the density times the volume; hence, the amount of energy it contains is:

AE = epn. VAt dS. (3.19)

To account for this energy flux, it is necessary to sum only the differential areas dS over the entire surface of the control volume, which is abbreviated as CS. That is, CS is the area of the bounding surface containing the volume CV. Notice that both of the required corrections to the energy in the system are provided because n. V is positive for the part going out of the control volume that must be added; n. V is negative for the flow of new energy into the control volume from upstream that must deducted. Therefore, the system energy at t + At is:

The surface term can be removed from the limit process because the At divides out. Then, using the fundamental definition for a derivative, we find that:

where partial-differentiation notation is used because the quantities inside the inte­grals may vary spatially as well as temporally. Expressed in words, Eq. 3.22 indicates that the rate of change of the energy in a system of particles is the sum of the rate of change of the energy residing at a given time within an arbitrarily chosen control volume that encompasses the system, plus the flux of energy through the surface bounding the control volume.

Notice that the integrands are composed of the intensive property (in this case, the energy per unit mass, e’) multiplied by other factors that describe the local flow field and fluid properties. In the volume integral, the factor is simply the mass of a volume element so that the integration gives the energy contained within the control volume. In the surface integral, e’ is multiplied by the factor n «V pdS = dm/dt=гіг, which can be interpreted as the mass flow rate through the differential area element at any location on the surface. Then, multiplying this by the energy per unit mass gives the flux of energy per unit area through the surface. Integration yields the net flux of energy from the control volume. The combination of the volume and the surface integrals then represents the time rate of change of the extensive property E, whose corresponding intensive property is e.

It is easy to see that we can replace E and e’ by any other pair of extensive variables (e. g., the pairs identified in Table 3.1). Then, we can use this tool to trans­form the fundamental laws of nature into the useful control-volume form for solving fluid-mechanics or aerodynamics problems. Writing Eq. 3.22 in general form, for any extensive property (e. g., J and its corresponding intensive property j), we have the Reynolds’ Transport Theorem:

It is now used to write each of the required natural laws in control-volume form in the manner described previously for the energy. In the discussions in the following sub­sections, the student will gain full confidence in this representation of fluid motion. However, the student will see that there are inherent limitations that characterize this approach. Later in the chapter, we pass to the differential-equation formulation of fluid dynamics to overcome these limitations. Nevertheless, the control-volume formulation provides useful insight into many basic fluid-flow problems of practical interest. In what follows, each law is recast in control-volume form, and the appli­cation of the results is demonstrated in a series of examples.

General form (Eq. 3.24)	dt JJJ pdV + JJ n-VpdS = 0
	v S
Steady compressible flow	JJ n – V pdS = 0 S	(3.25)
Incompressible flow	JJ n-V dS = 0	(3.26)
	S

Table 3.2. Continuity equation in control-volume form

Conservation of Mass: The Continuity Equation

For the mass of the system of particles to stay constant, Eq. 3.1 must be satisfied. Then, in control-volume form, using the Reynolds’ Transport Theorem and noting that the extensive property is simply unity as shown in Table 3.1, it is necessary that:

This is the general control-volume statement of the continuity equation. It remains to apply this equation in a variety of situations to illustrate its utility in problem solving. Before discussing actual problems, it is useful to define several special cases that frequently arise. For example, in many problems, the flow is steady—that is, the properties at a given location in the flow field may not change with time. Then, the volume integral does not change with time and its derivative vanishes. In other situ­ations, the flow may be incompressible, in which case the density p is constant and can be removed from the integrals. Table 3.2 summarizes several special cases of interest.

Notice that the equation for incompressible flow holds for both steady and unsteady flows because the volume of the control volume does not change with time. The constant density can be factored out of the equation and the derivative term vanishes whether or not the flow is time-dependent. The notations CV and CS indicating the volume and surface of integration often are replaced with Vand S, as shown in the table; there is no difference in meaning.